Предмет: Алгебра,
автор: zhanik73
Решение систем неравенств. Урок 4
Срочно дам 40 баллов
Приложения:
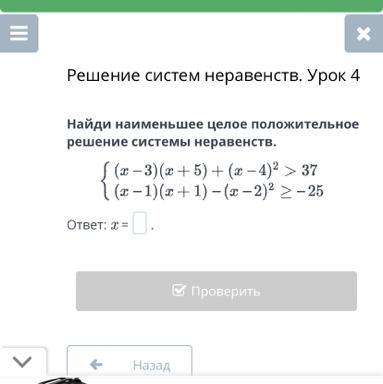
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: n0H
Предмет: Українська мова,
автор: andreybabich201009
Предмет: Українська мова,
автор: Аноним