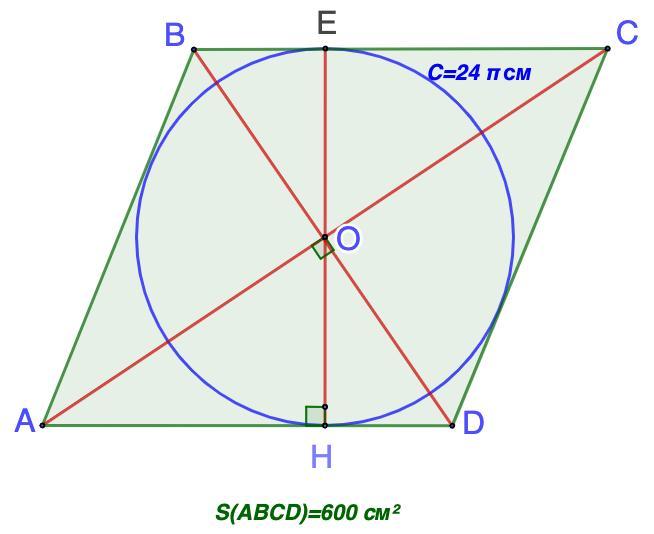
Площа ромба дорівнює 600 см², а довжина кола, вписаного в нього, дорівнює 24п. Обчислити меншу діагональ ромба.
Ответы
Ответ:
Меньшая диагональ ромба равна 30 см.
Объяснение:
Площадь ромба равна 600 см², а длина окружности, вписанной в него, равна 24π см. Вычислить меньшую диагональ ромба.
Дано: ABCD - ромб;
Окр.О - вписана;
С = 24π см; S(ABCD) = 600 см².
Найти: BD.
Решение:
Проведем высоту ЕН через центр Окр.О.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ЕН - диаметр окр.О.
- Длина окружности равна:
С = 2πR
24π = 2πR ⇒ R = 12 см.
- Диаметр равен двум радиусам.
⇒ ЕН = 24 см.
- Площадь ромба равна:
S = ah,
где а - сторона ромба, h - высота ромба.
⇒ S(ABCD) = AD · EH
600 = AD · 24 ⇒ AD = 600 : 24 = 25 (см)
Рассмотрим ΔAOD.
- Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
⇒ ΔAOD - прямоугольный.
ОН = 12 см - высота.
- Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу.
⇒ ОН² = АН · НD
Пусть HD = x см, тогда АН = (25 - х) см.
144 = (25 - х) · х
х² - 25х + 144 = 0
D = 625 - 576 = 49 ⇒ √D = 7
⇒ HD = 9 см; АН = 25 - 9 = 16 (см)
Рассмотрим ΔНОD - прямоугольный.
- Теорема Пифагора:
- Квадрат гипотенузы равен сумме квадратов катетов.
OD² = HD² + OH² = 81 + 144 = 225 ⇒ OD = 15 см
BD = 2 · OD = 30 см
#SPJ1