Предмет: Геометрия,
автор: Dillrez
Поставлю ЛУЧШИЙ ОТВЕТ - за полное решение.
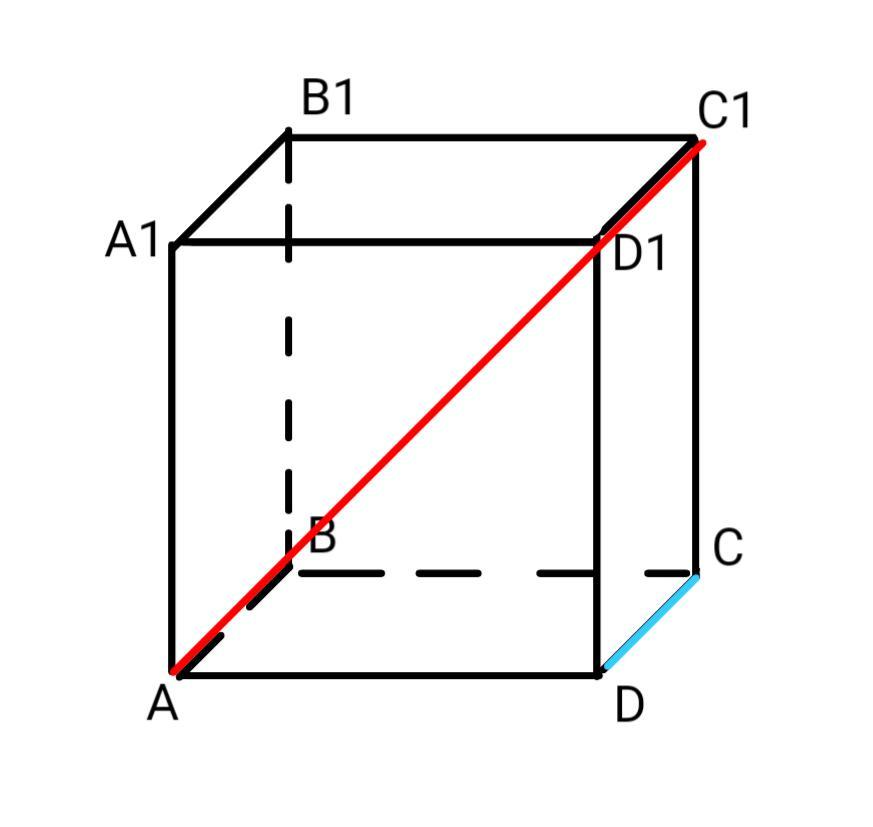
Задача: Дан куб ABCDA1B1C1D1, ребро куба - a. Найти расстояние между прямыми AC1 и CD
Приложения:
ГАЗ52:
Вай фай появился. Могу сделать. Делать?
Почему? Если брать и проводить перпендикуляр с CD то нужно просто подобрать угол к AC1 так, чтоб было перпендикулярно.
То есть просто можно менять угол относительно AC1, но прямая всё равно останется перпендикулярной к CD.
Подбирать угол будешь по правилам геометрии, так что отрезок ( у меня) РК должен быть одновременно перпендикулярен 2 прямым.
Вернёшься к первоначальному варианту
Тот вариант я изначально понял, у меня просто в голове вопрос такой возник.
Я могу Вам написать где будет удобно, чтоб показать, что я имею ввиду.
Можно писать здесь.
Так здесь просто сложно описать, я б на примере картинки показал, что имею ввиду
Теорема: две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
Ответы
Автор ответа:
1
Расстояние между скрещивающимися прямыми - длина общего перпендикуляра.
Cкрещивающиеся прямые лежат в параллельных плоскостях.
Общий перпендикуляр будет расстоянием между плоскостями.
Проведем через AC1 плоскость, параллельную CD.
Если прямая параллельна прямой в плоскости, то она параллельна плоскости.
CD||C1D1 => CD||(AC1D1)
Найдем расстояние от прямой CD до плоскости (AC1D1).
Проведем DO⊥AD1
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в плоскости.
C1D1⊥(ADD1) => C1D1⊥DO
Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна плоскости.
DO⊥AD1, DO⊥С1D1 => DO⊥(AC1D1)
DO - искомое расстояние
DO=AD/√2 =a/√2 (половина диагонали квадрата AA1D1D)
Приложения:

Не совсем его понял, но мы действительно опускаем перпендикуляр на параллельную плоскость из любой точки прямой CD - там, где нам удобно его доказать и найти
Мы ищем расстояние между скрещивающимися прямыми как расстоние между паралельными плоскостями, в которых лежат эти прямые. А расстояние между плоскостями как расстояние между прямой и плоскостью или между точкой и плоскостью.
Он считает, что таких перпендикуляров он может построить много
Две скрещивающиеся прямые имеют единственный общий перпендикуляр.
Но нам не обязательно находить именно его. Достаточно найти расстояние между плоскостями, которому он равен.
Понятно..., не удалось убедить в этом Dillrez.
reader.lecta.rosuchebnik.ru/demo/7999/data/chapter18.xhtml
Коротко: если есть два общих перпендикуляра, то через них проходит плоскость и скрещивающиеся прямые будут её следами в параллельных плоскостях, то есть параллельными прямыми - противоречие.
Ясно. Спасибо.
Благодарен Вам за ответ и объяснение)
Похожие вопросы
Предмет: Физика,
автор: ginichimarurol
Предмет: Русский язык,
автор: RAMENCHIKS
Предмет: История,
автор: yaroslavka1308
Предмет: Музыка,
автор: Don1A