ДАЮ ВЕЛИКУ КІЛЬКІСТЬ БАЛІВ.
У зірки Бетельгейзе (a Оріона) річний паралакс дорівнює 0,012′′, власний рух 0,032′′ і променева швидкість дорівнює +21 км/с. Визначте модуль просторової швидкості зірки. а) 33,4 км/с; г) 13,4 км/с; б) 24,6 км/с; д) 10,3 км/с. в) 27,3 км/с;
Дуже потрібна відповідь з поясненнями та формулами
Ответы
Ответ: Вариант ответа б) модуль скорости ≈ 24,6 км/с.
Объяснение: Дано:
Годовой параллакс Бетельгейзе р′′ = 0,012′′
Собственное движение звезды а′′ = 0,032′′
Лучевая скорость звезды Vлуч. = +21 км/с.
Найти модуль пространственной скорости звезды Vполн.-?
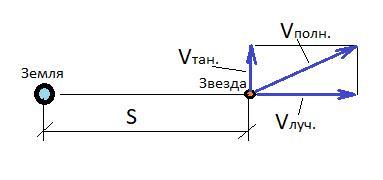
Смотрите рисунок.
Чтобы найти Vполн. вначале надо найти тангенциальную скорость звезды (Vтан.), т.е. скорость, перпендикулярную лучу зрения. Для этого надо знать расстояние до звезды. Расстояние в парсеках определяется выражением:
Sпк = 1/р′′. Так как в одном парсеке содержится 206265 астрономических единиц, то расстояние Sпк в астрономических единицах будет равно:
Sа.е. = Sпк*206265 = 206265/ р′′.
С такого расстояния линейное перемещение (L) звезды за год видно под углом а′′, следовательно, можно найти это линейное расстояние. В астрономических единицах оно будет равно:
L = а′′*Sа.е./206265 = а′′*206265/р′′*206265 = а′′/р′′
Таким образом, за год звезда перемещается перпендикулярно лучу зрения на L= а′′/р′′ = 0,032′′/0,012′′ =
= 2,(6) а.е.
Так как одна астрономическая единица = 149600000 км, то годовое перемещение звезды в километрах в направлении перпендикулярном лучу зрения будет равно: Lкм = L*149600000 = 398933333, (3) км.
В году содержится секунд N = 365,25*24*60*60 = 31557600 секунд. Тогда тангенциальная скорость звезды будет равна Vтан = Lкм/N = 398933333, (3)/31557600 ≈ 12,641км/с.
Модуль полной пространственной скорости звезды найдем по теореме Пифагора: Vполн² = Vлуч² + Vтан².
Отсюда Vполн=√(Vлуч² + Vтан²)=√(21² + 12,641²) ≈ 24,51 км/с
Из приведенных вариантов ответов подходит вариант б)