Предмет: Геометрия,
автор: Sombrasueno
Все двугранные углы при основании пирамиды равны 60 градусов. Найдите площадь основания пирамиды, если Боковая поверхность ее равна 36
Ответы
Автор ответа:
0
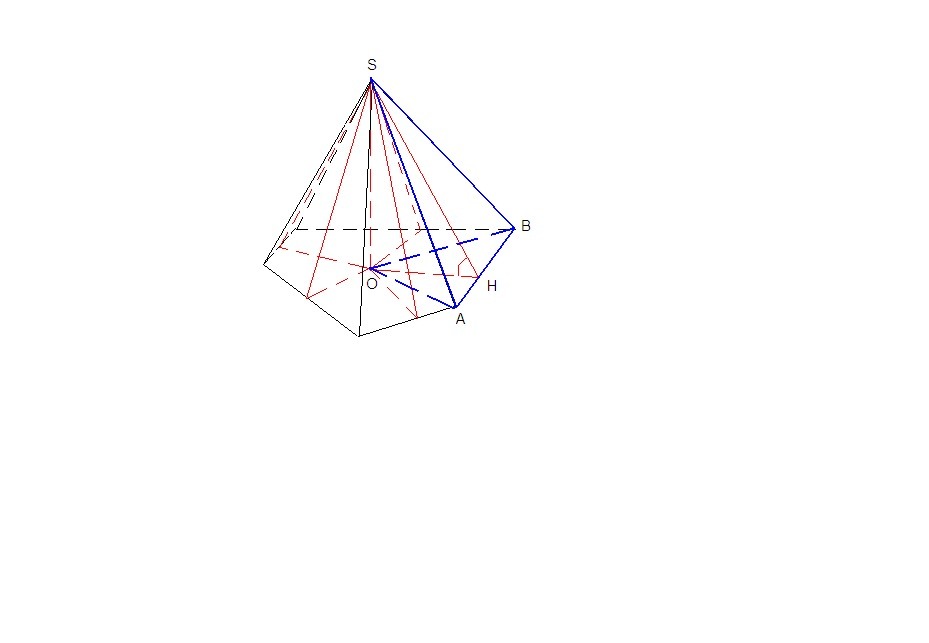
Пусть SO высота пирамиды.
Для грани SAB построим линейный угол двугранного угла. Для этого проведем из точки О перпендикуляр ОН к ребру основания АВ. ОН - проекция SH на плоскость основания, значит SH⊥AB по теореме о трех перпендикулярах.
∠SHO = 60° - линейный угол двугранного угла.
Аналогично строим линейные углы наклона всех боковых граней.
SΔaob = АВ · ОН / 2
SΔsab = AB · SH / 2
Saob / Ssab = OH / SH = cos∠SHO = cos60° = 1/2
Saob = Ssab/2
Так как все боковые грани наклонены под одним углом, для каждой боковой грани и ее проекции мы получим такое же отношение.
Значит, площадь основания равна половине площади боковой поверхности:
Sосн = Sбок/2 = 36/2 = 18
Для грани SAB построим линейный угол двугранного угла. Для этого проведем из точки О перпендикуляр ОН к ребру основания АВ. ОН - проекция SH на плоскость основания, значит SH⊥AB по теореме о трех перпендикулярах.
∠SHO = 60° - линейный угол двугранного угла.
Аналогично строим линейные углы наклона всех боковых граней.
SΔaob = АВ · ОН / 2
SΔsab = AB · SH / 2
Saob / Ssab = OH / SH = cos∠SHO = cos60° = 1/2
Saob = Ssab/2
Так как все боковые грани наклонены под одним углом, для каждой боковой грани и ее проекции мы получим такое же отношение.
Значит, площадь основания равна половине площади боковой поверхности:
Sосн = Sбок/2 = 36/2 = 18
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: poyda7689
Предмет: Химия,
автор: ali8133
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: lessikonchik
Предмет: Алгебра,
автор: ameria46