Предмет: Математика,
автор: Volodimir
Помогите срочно решить!
Приложения:
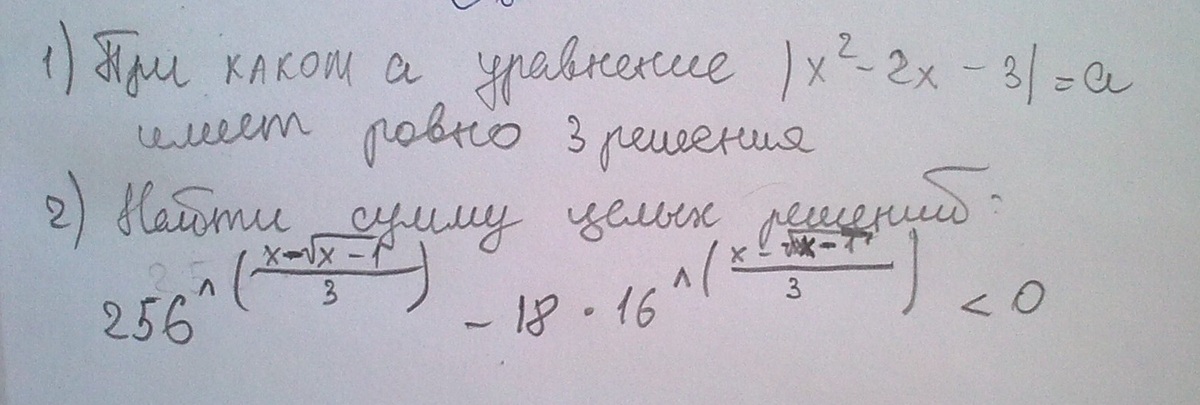
Ответы
Автор ответа:
0
1) Проанализируем функцию ![y=|x^2-2x-3|\\
1)\
x^2-2x-3 geq 0\
(x-3)(x+1) geq 0\
--------------->x\
-1 0 [3] \
(-oo;-1] U [3;+oo)\\
2)\
x^2-2x-3 < 0\
(x-3)(x+1) < 0\
----------------->x\
-1 3 \
(-1;3) y=|x^2-2x-3|\\
1)\
x^2-2x-3 geq 0\
(x-3)(x+1) geq 0\
--------------->x\
-1 0 [3] \
(-oo;-1] U [3;+oo)\\
2)\
x^2-2x-3 < 0\
(x-3)(x+1) < 0\
----------------->x\
-1 3 \
(-1;3)](https://tex.z-dn.net/?f=y%3D%7Cx%5E2-2x-3%7C%5C%5C%0A1%29%5C%0Ax%5E2-2x-3+geq+0%5C%0A%28x-3%29%28x%2B1%29+geq+0%5C%0A---------------%26gt%3Bx%5C%0A+++-1++++++0++++++++++%5B3%5D+%5C%0A%28-oo%3B-1%5D+U++%5B3%3B%2Boo%29%5C%5C%0A2%29%5C%0Ax%5E2-2x-3+%26lt%3B+0%5C%0A%28x-3%29%28x%2B1%29+%26lt%3B+0%5C+%0A+-----------------%26gt%3Bx%5C%0A+++++++-1++++++++++3+%5C%0A+%28-1%3B3%29)
Так как график функций не не четен и не четен .
То она представляет собой график который расположен (в силу условия модуля) выше оси абсцисс ОХ.
Найдем точки убывания и возрастания

Откуда получаем что функция
Возрастает на отрезке
![[-1;1] U [3;+oo)\ [-1;1] U [3;+oo)\](https://tex.z-dn.net/?f=%5B-1%3B1%5D+U++%5B3%3B%2Boo%29%5C)
Убывает на отрезке
![(-oo;-1] U [1;3] (-oo;-1] U [1;3]](https://tex.z-dn.net/?f=%28-oo%3B-1%5D+U++%5B1%3B3%5D)
Теперь очевидно что функция будет иметь ровно три корня когда будет пересекать функцию слева в точке возрастания а точнее в точке

подставляем в нашу функцию

то есть при , уравнение будет иметь ровно три корня. И они равны
, уравнение будет иметь ровно три корня. И они равны

2)Заменим
откуда получаем интервал решения в целых числах так как там интервал
 это будет решение обеих неравенств
это будет решение обеих неравенств
сумма целых равна
Так как график функций не не четен и не четен .
То она представляет собой график который расположен (в силу условия модуля) выше оси абсцисс ОХ.
Найдем точки убывания и возрастания
Откуда получаем что функция
Возрастает на отрезке
Убывает на отрезке
Теперь очевидно что функция будет иметь ровно три корня когда будет пересекать функцию слева в точке возрастания а точнее в точке
подставляем в нашу функцию
то есть при
2)Заменим
откуда получаем интервал решения в целых числах так как там интервал
сумма целых равна
Похожие вопросы
Предмет: История,
автор: nekomanya
Предмет: Математика,
автор: bsalma2010
Предмет: Русский язык,
автор: yaxochydva
Предмет: Алгебра,
автор: daruk
Предмет: Химия,
автор: Fataked