Предмет: Геометрия,
автор: secretik31
РЕШИТЕ ПОЖАЛУЙСТА 221. найдите площадь полной поверхности равностороннего конуса, высота которого равна 2√3 см.
Ответы
Автор ответа:
1
Дано:
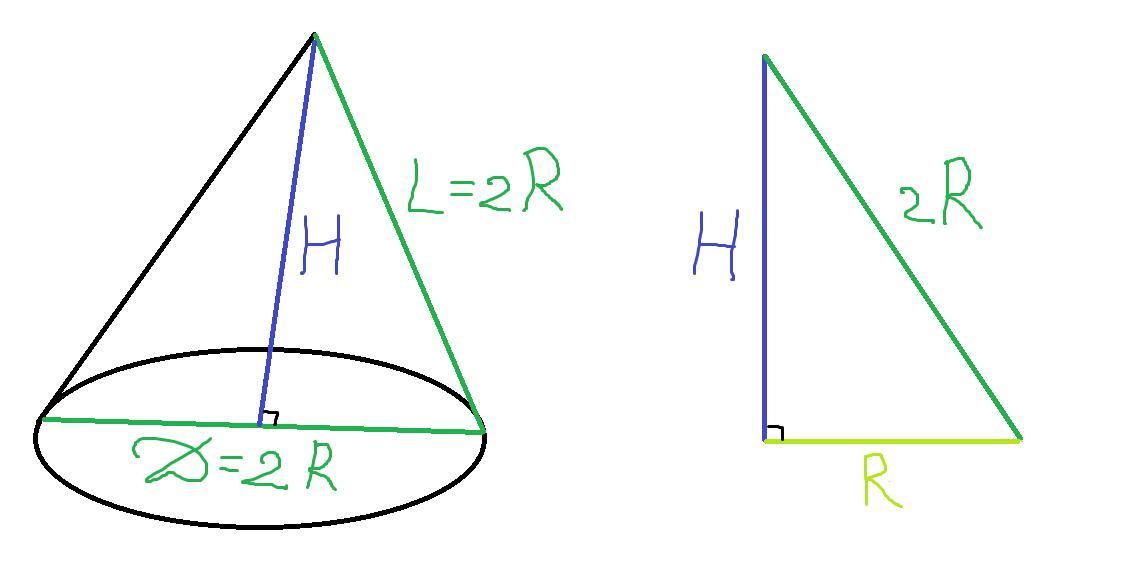
Равносторонний конус;
H = 2√3 см
Найти: S(полн) - ?
Решение:
Равносторонний конус - конус, образующая и диаметр основания которого равны:
L = D = 2R
Рассмотрим осевое сечение конуса. Радиус основания, высота и образующая составляют прямоугольный треугольник. Запишем для него теорему Пифагора:
Используя условие о том, что образующая и диаметр основания равностороннего конуса равны, получим:
Площадь полной поверхности конуса определяется по формуле:
Преобразуем эту формулу, учитывая, что конус равносторонний:
Находим площадь полной поверхности:
Ответ: 12п см²
Приложения:
secretik31:
благодарю
223. радиусы оснований усеченного конуса равны 2 см и 4см. найдите площадь сечения этого усеченного конуса плоскостью, параллельной основаниям и проходящей через середину его высоты.
можете помочь еще с этим
ято такое rifgradrof?
Похожие вопросы
Предмет: Алгебра,
автор: kononenkos193
Предмет: Литература,
автор: mariakonik471
Предмет: Физика,
автор: toxirovabduraxmon140
Предмет: Математика,
автор: Burunov2002