Предмет: Алгебра,
автор: porplicza2018
Яка з функцій парна?
Приложения:
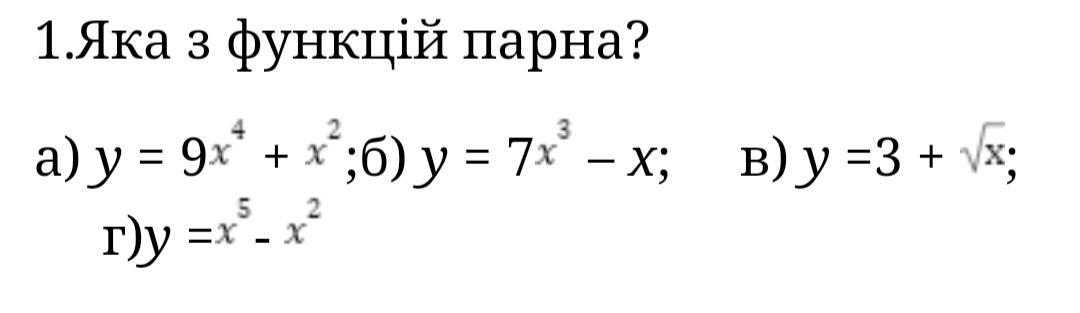
teacher1011:
а)
Ответы
Автор ответа:
0
Відповідь: а
Пояснення:
а)
За визначенням парності функції: , отже функція парна за f(x)=f(-x). Це пояснюється тим, що всі змінні мають парний степінь, відповідно
.
б)
Ця функція непарна за f(-x) = -f(x), але це не чого вимагало завдання. Тут, зауважу, що мінус зберігається бо степінь - непарне число.
в) , дана функція не є ні парною, ні непарною.
г) - ні парна, ні непарна.
Похожие вопросы
Предмет: Математика,
автор: aelagina08
Предмет: Другие предметы,
автор: tkacuko456
Предмет: Английский язык,
автор: sprite4i
Предмет: Математика,
автор: annachernaya281514
Предмет: Геометрия,
автор: KarinaOlifirenko