Предмет: Алгебра,
автор: alisa34289
Розв'яжіть систему нерівностей
Приложения:
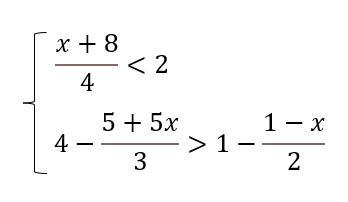
Ответы
Автор ответа:
0
Ответ:
Множество решений системы неравенств (-∞; 0)
Объяснение:
Перевод: Решите систему неравенств
Информация: Если a > b (или a < b), c > 0, то a·c > b·c (или a·c < b·c).
Решение. Обе части первого уравнения умножим на положительное число 4, а обе части второго уравнения умножим на положительное число 6=3·2, а потом упростим.
Определим множество решений каждого неравенства:
Так как рассматривается система, то находим пересечение множеств решений:
x ∈ (-∞; 0).
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: Katerina24575
Предмет: Информатика,
автор: gggd1024
Предмет: Математика,
автор: stroynastya
Предмет: Русский язык,
автор: mariaalaverdin
Предмет: Русский язык,
автор: YouMyGalaxy