Предмет: Алгебра,
автор: soliababiuk
знайти похідну y= cos x+sin π/6
Ответы
Автор ответа:
0
Щоб знайти похідну функції y = cos(x) + sin(π/6), ми можемо диференціювати кожен член окремо, використовуючи правила диференціювання.
Похідна cos(x) дорівнює -sin(x), а похідна sin(π/6) дорівнює 0, оскільки є сталою.
Отже, похідна у відносно х дорівнює:
dy/dx = d(cos(x))/dx + d(sin(π/6))/dx
= -sin(x) + 0
= -sin(x)
Отже, похідна y за x дорівнює -sin(x).
Розв'язок задачі має вигляд dy/dx = -sin(x).
Похідна cos(x) дорівнює -sin(x), а похідна sin(π/6) дорівнює 0, оскільки є сталою.
Отже, похідна у відносно х дорівнює:
dy/dx = d(cos(x))/dx + d(sin(π/6))/dx
= -sin(x) + 0
= -sin(x)
Отже, похідна y за x дорівнює -sin(x).
Розв'язок задачі має вигляд dy/dx = -sin(x).
Автор ответа:
0
Ответ:
дай лучший ответ пж
Объяснение:
Приложения:
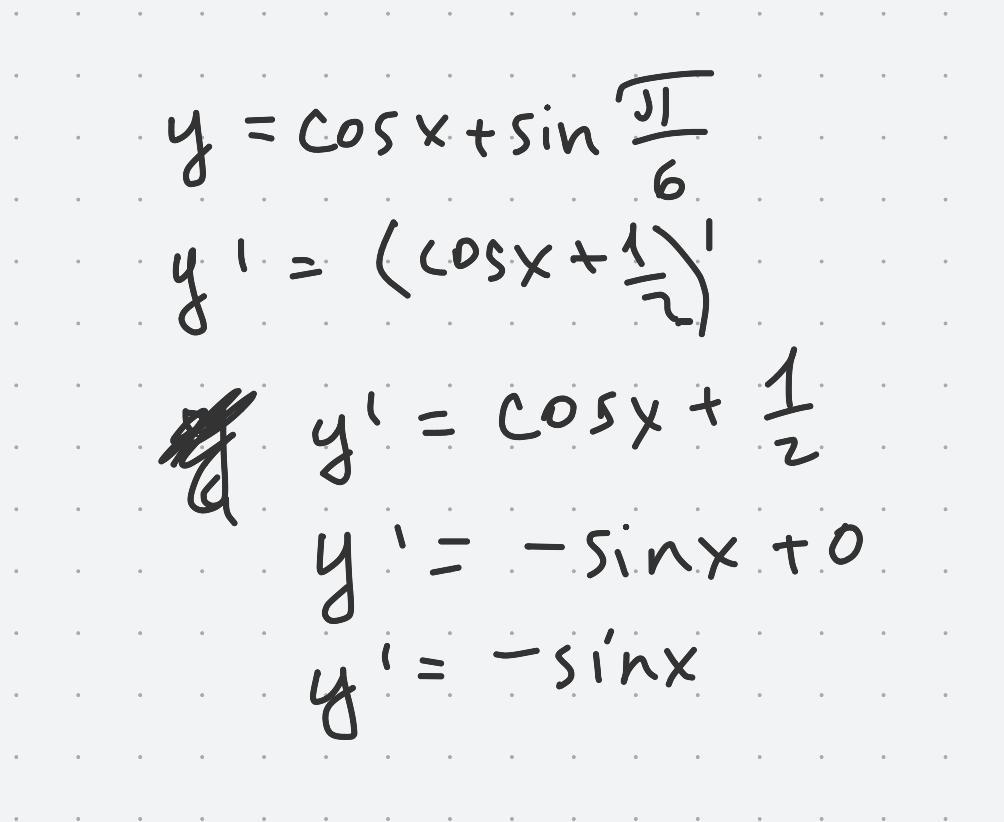
Похожие вопросы
Предмет: История,
автор: mnepopik46
Предмет: Информатика,
автор: x3668419
Предмет: Українська мова,
автор: oparinamiroslava1
Предмет: Химия,
автор: golikov3200
Предмет: Английский язык,
автор: Morgandi321