Предмет: Алгебра,
автор: pekka1096
ДОПОМОЖІТЬ БУДЬ ЛАСКА !!!!
Приложения:
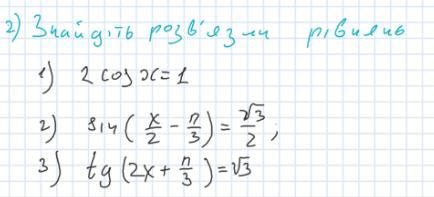
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решить уравнения.
Решим уравнения.
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: nahorniyartemka
Предмет: Другие предметы,
автор: sumarinaanna451
Предмет: Алгебра,
автор: jsbsvysusmsj
Предмет: Математика,
автор: goodpomoshnoc