Question

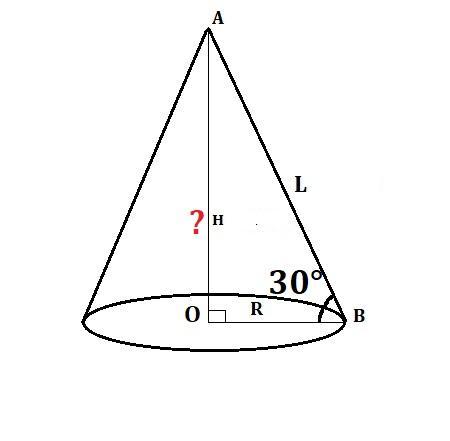
Довжина кола основи конуса дорівнює 36π, твірна нахилена до площини основи під кутом 30 градусів. Знайдіть висоту конуса.

Answer 1

Ответ:

Висота конуса дорівнює 6√3 ед

Пошаговое объяснение:

Довжина кола основи конуса дорівнює 36π, твірна нахилена до площини основи під кутом 30°. Знайдіть висоту конуса.

Маємо конус з висотою Н=АО, в основі якого лежить круг, довжина кола якого дорівнює 36π.

L=АВ - твірна конуса.

∠В - кут між твірною і радіусом основи конуса ОВ=R – кут нахилу твірної до площини основи конуса. ∠В = 30°

Розв'язання

1)Довжину кола можна знайти за формулою:

C=2πR.

Звідси:  2πR=36π, тому R=18.

Отже, ОВ=R=18 (ед)

2) З прямокутного трикутника AOB за означенням тангенса гострого кута прямокутного трикутника:

$\bf tg\angle B =\dfrac{AO}{OB}$

$\sf AO=OB\cdot tg30^\circ = 18\cdot \dfrac{\sqrt{3} }{3} =\bf 6\sqrt{3}$  (ед)

Відповідь:  6√3 ед

#SPJ1