решите систему неравенств 50 баллов дам
х²-3х+9>0
х²⩽36
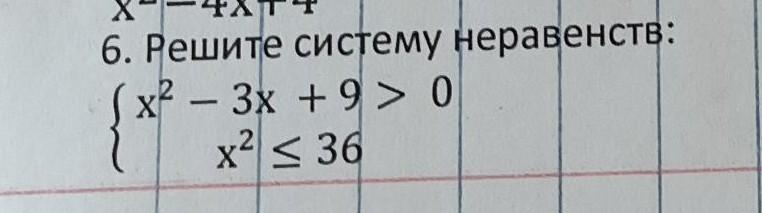
Ответы
Ответ:
Розв'яжемо
1) x² - 3x + 9 > 0
Для початку знайдемо корені квадратного рівняння x² - 3x + 9 = 0. Використаємо формулу дискримінанту:
D = b² - 4ac = (-3)² - 4·1·9 = 9 - 36 = -27
Якщо дискримінант від'ємний, то рівняння не має дійсних коренів. Оскільки коефіцієнт a = 1 (додатній), то це означає, що квадратний термін завжди буде додатнім. Тому рівняння x² - 3x + 9 = 0 не має дійсних коренів, а отже, його знак не змінюється на відрізку між коренями. Отримаємо верхню межу цього виразу:
x² - 3x + 9 > 0 ⇔ x ∈ (-∞, ∞)
Отже, розв'язок першої нерівності - це всі дійсні числа.
2) x² ⩽ 36
Зведемо нерівність до канонічного вигляду:
x² - 36 ⩽ 0
Розв'яжемо рівняння x² - 36 = 0, знайдемо корені:
x₁ = -6, x₂ = 6
Отже, на відрізку [-6, 6] функція x² - 36 змінює знак з "плюс" на "мінус". Оскільки коефіцієнт a = 1 (додатній), то це означає, що функція x² - 36 завжди менше нуля на відрізку (-∞, -6) ∪ (6, ∞), а на відрізку [-6, 6] вона менше або дорівнює нулю. Отримаємо нижню межу цього виразу:
x² ⩽ 36 ⇔ x ∈ [-6, 6]
Отже, розв'язок другої нерівності - це відрізок [-6, 6].
Отже, розв'язок системи нерівностей - це перетин розв'язків кожної окремої нерівності, тобто відрізок [-6, 6].