Предмет: Геометрия,
автор: ixpxhxoxnxex
Решите всё даю 26 баллов больше нету
Приложения:

Ответы
Автор ответа:
0
Часть С
3. Т.к. AN II MB, то углы ANM и NMB равны как накрест лежащие углы при пересечении двух параллельных прямых AN и MB секущей MN.
Углы NAD и ABM также равны как накрест лежащие углы при пересечении двух параллельных прямых AN и MB секущей АВ.
AN = ВМ по условию.
Значит, треугольники равны по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соответственно равна стороне и двум прилежащим к ней углам другого треугольника.
4. После построения отрезков мы получаем два равных треугольника РВК и РDК. Они равны по третьему признаку равенства треугольников: РВ = DК по условию, ВК = PD по условию, сторона РК - общая. При наложении такие треугольники полностью совместятся. Значит, ВК II DP.
5. Треугольники АСЕ и АВD - подобны по первому признаку подобия треугольников: угол А - общий, углы АСЕ и АВD равны как соответственные углы при пересечении двух параллельных СЕ и BD секущей АВ. Значит, углы треугольника АСЕ равны углам АВD:
< ACE = < B = 76°
< AEC = ADB = 52°
Зная, что сумма углов треугольника равна 180, находим угол А:
BAD = 180 - 76 - 52 = 52°
Часть С:
3. Получившиеся треугольники равны по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соттветственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. В нашем случае:
AD = BE по условию.
BD - общая сторона
Углы ADB и DBE равны как накрест лежащие углы при пересечении двух параллельных прямых ВЕ и AD секущей BD.
Т.к. треугольники равны, то АВ = DE = 5 см
4. Треугольники АВС и МКВ подобны по первому признаку подобия: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. В нашем случае:
угол В - общий. Углы ВМК и ВАС равны как соответственные углы при пересечении параллельных прямых МК и АС секущей АВ.
Значит, углы треугольника МКВ равны углам треугольника АВС:
<MKB = ACB = 66°
< B = 48°
Находим угол ВМК:
<BMK = 180 - 66 - 48 = 66°
5. У нас получилось два треугольника АОВ и ОВК.
Рассмотрим углы АВО и ВОК. Они - накрест лежащие углы при пересечении двух параллельных прямых АС и МК секущей ВО. Значит, эти углы равны.
Углы СВО и МОВ также равны как накрест лежащие углы при пересечении двух параллельных прямых АС и МК секущей ВО. По условию ОА и ВК - биссектрисы, поэтому и углы КВО и АОВ - равны между собой.
Сторона ВО - общая.
Таким образом, треугольники АОВ и ОВК равны между собой по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника. При наложении треугольники полностью совместятся. Значит, AO II BK
3. Т.к. AN II MB, то углы ANM и NMB равны как накрест лежащие углы при пересечении двух параллельных прямых AN и MB секущей MN.
Углы NAD и ABM также равны как накрест лежащие углы при пересечении двух параллельных прямых AN и MB секущей АВ.
AN = ВМ по условию.
Значит, треугольники равны по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соответственно равна стороне и двум прилежащим к ней углам другого треугольника.
4. После построения отрезков мы получаем два равных треугольника РВК и РDК. Они равны по третьему признаку равенства треугольников: РВ = DК по условию, ВК = PD по условию, сторона РК - общая. При наложении такие треугольники полностью совместятся. Значит, ВК II DP.
5. Треугольники АСЕ и АВD - подобны по первому признаку подобия треугольников: угол А - общий, углы АСЕ и АВD равны как соответственные углы при пересечении двух параллельных СЕ и BD секущей АВ. Значит, углы треугольника АСЕ равны углам АВD:
< ACE = < B = 76°
< AEC = ADB = 52°
Зная, что сумма углов треугольника равна 180, находим угол А:
BAD = 180 - 76 - 52 = 52°
Часть С:
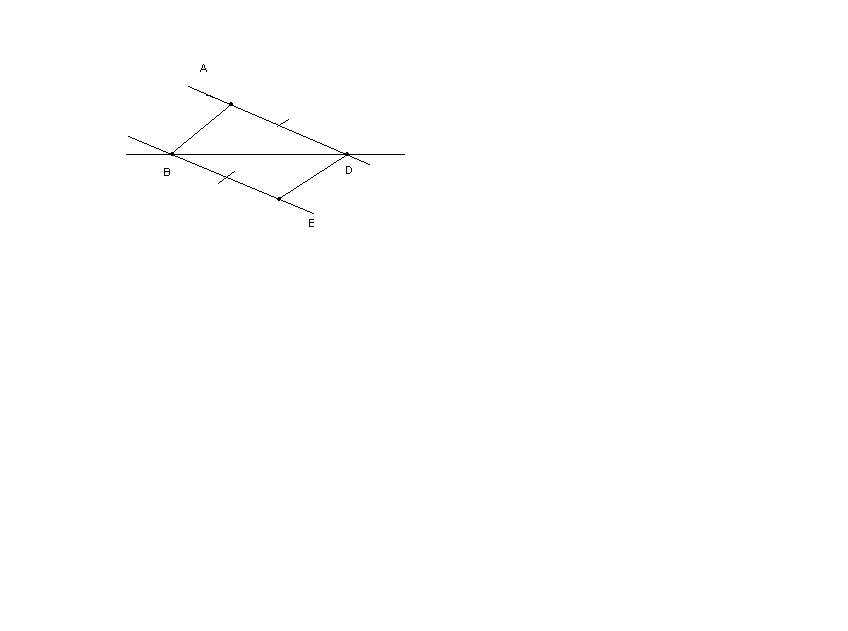
3. Получившиеся треугольники равны по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соттветственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. В нашем случае:
AD = BE по условию.
BD - общая сторона
Углы ADB и DBE равны как накрест лежащие углы при пересечении двух параллельных прямых ВЕ и AD секущей BD.
Т.к. треугольники равны, то АВ = DE = 5 см
4. Треугольники АВС и МКВ подобны по первому признаку подобия: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. В нашем случае:
угол В - общий. Углы ВМК и ВАС равны как соответственные углы при пересечении параллельных прямых МК и АС секущей АВ.
Значит, углы треугольника МКВ равны углам треугольника АВС:
<MKB = ACB = 66°
< B = 48°
Находим угол ВМК:
<BMK = 180 - 66 - 48 = 66°
5. У нас получилось два треугольника АОВ и ОВК.
Рассмотрим углы АВО и ВОК. Они - накрест лежащие углы при пересечении двух параллельных прямых АС и МК секущей ВО. Значит, эти углы равны.
Углы СВО и МОВ также равны как накрест лежащие углы при пересечении двух параллельных прямых АС и МК секущей ВО. По условию ОА и ВК - биссектрисы, поэтому и углы КВО и АОВ - равны между собой.
Сторона ВО - общая.
Таким образом, треугольники АОВ и ОВК равны между собой по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника. При наложении треугольники полностью совместятся. Значит, AO II BK
Приложения:



Автор ответа:
0
Ага. Мозги тренить нужно, иначе начнется преждевременный маразм
Автор ответа:
0
ну да :))
Автор ответа:
0
тебе дались баллы?
Автор ответа:
0
Фиг знает, я обычно туда не смотрю, где они даются
Автор ответа:
0
понятно ясно
Похожие вопросы
Предмет: Химия,
автор: artemdereka
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: nevgadaesh007
Предмет: Геометрия,
автор: katherine5689
Предмет: Литература,
автор: Dasha0711