Предмет: Алгебра,
автор: dragonbool597
Помогите пожалуйста 6. Розв'яжiть рiвняння: (на фото)
Приложения:
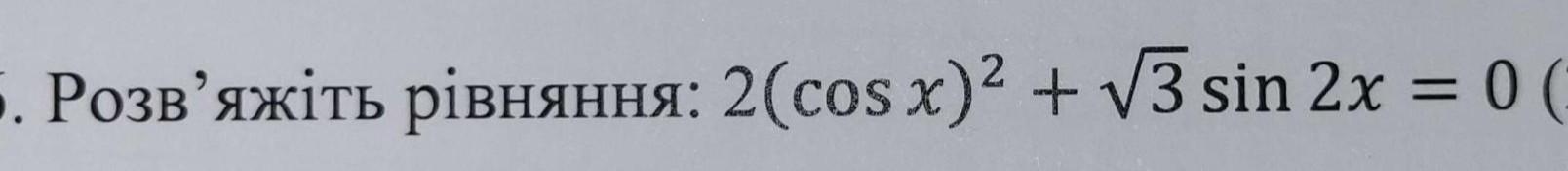
Ответы
Автор ответа:
1
Пояснення:
Похожие вопросы
Предмет: Литература,
автор: novsi2423
Предмет: История,
автор: chebirechek
Предмет: Математика,
автор: feruzaangiboeva0
Предмет: Математика,
автор: gerardnasway
Предмет: Право,
автор: QVEHOD