Предмет: Геометрия,
автор: lukerose1arz
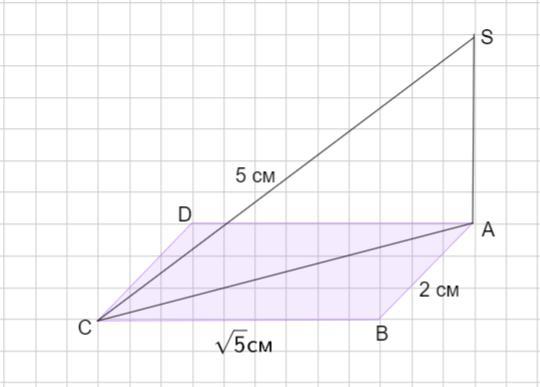
Через точку А прямокутника ABCD проведено перпендикуляр SA до площини ABC. Знайдіть SA, якщо SC = 5 см, а сторони прямокутника дорівнює 2см і √5 см
Ответы
Автор ответа:
1
Ответ:
SA = 4 cм.
Объяснение:
Через точку А прямоугольника ABCD проведен перпендикуляр SA к плоскости АВС Найти SA, если SC = 5 см , а стороны прямоугольника равны 2 см и √ 5 см.
Пусть дан прямоугольник ABCD . SA ⊥ (АВС) .
АВ =2см, ВС =√ 5см. SC = 5 см.
Так как ABCD - прямоугольник, то ΔАВС - прямоугольный. Найдем АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АС² = АВ² +ВС ²;
АС² = 2² +(√5)² = 4 +5 = 9;
АС =√9 = 3 см.
Если SA ⊥ (АВС) , то она перпендикулярна и прямой АС .
ΔSAС - прямоугольный. Применим теорему Пифагора .
SC² = SA² + AC²;
SA² = SC² - AC²;
SA² = 5² - 3² = 25 - 9 = 16;
SA = √16 = 4 cм.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: madinaturlan
Предмет: История,
автор: mariamnurmatova655
Предмет: Геометрия,
автор: maskavlada510
Предмет: Физика,
автор: sasakrivulko98