x²+ 3x < 2 + x
яке з чисел є розв'язком нерівності
1) 1
2)0
3)5
розпишіть
Ответы
Ответ:
2) 0
Объяснение:
х² +3х < 2 +x .
Какое из чисел является решением неравенства
1) 1
2) 0
3) 5.
Решим данное неравенство. Для этого перенесем все слагаемые в левую часть
х² +3х < 2 +x ;
х² +3х- 2 - х < 0;
х² +2х - 2 < 0
Найдем корни квадратного трехчлена, решив уравнение:
х² +2х - 2 =0;
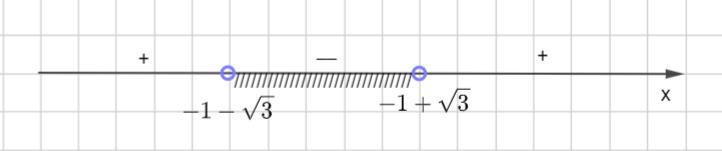
Тогда решением неравенства будет ( -1 -√3; - 1 +√3) ( во вложении)
Оценим концы полученного промежутка √3≈ 1,7
- 1 - √3≈ -2,7
- 1 + √3≈ 0,7
Тогда данному промежутку принадлежит число 0.
Значит, 2) 0 - является решением неравенства .
2 способ
х² +2х - 2 < 0
Проверим каждое значение. Для этого подставим каждое число и оценим числовое равенство.
1) х =1
1² +2 · 1 - 2 < 0 ;
1 < 0
Неравенство неверно. Значит, число 1 не является решением неравенства.
2) х=0
0² +2 · 0 - 2 < 0 ;
-2 < 0
Неравенство верно. Значит, число 0 является решением
3) х =5
5² +2 · 5 - 2 < 0 ;
33 < 0
Неравенство неверно. Значит, число 5 не является решением.
Значит, 2) 0 - решение неравенства
#SPJ1