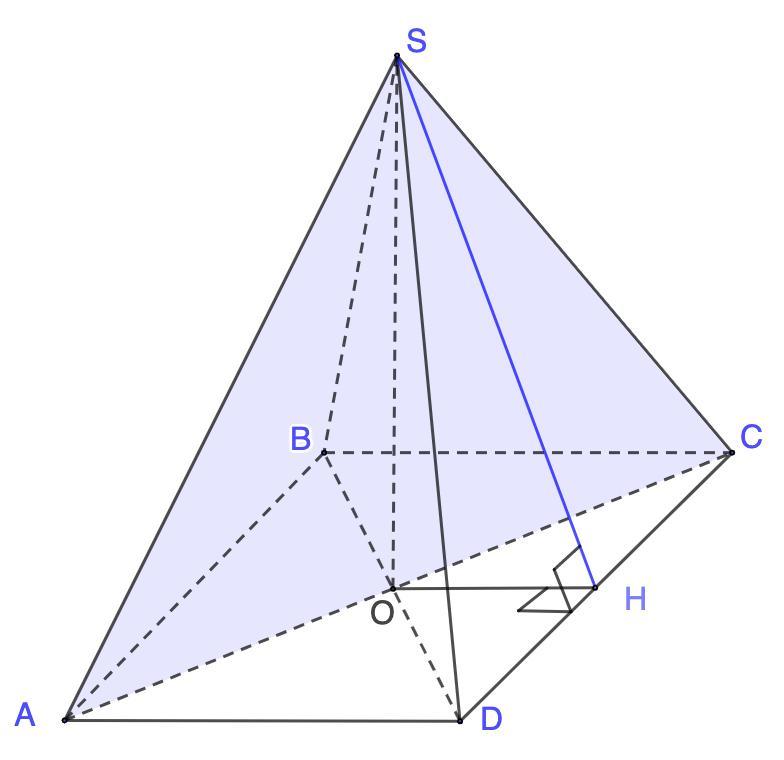
Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 104, а площадь полной поверхности этой пирамиды равна 120. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
Ответы
Ответ:
Площадь сечения равна 2√330 ед².
Объяснение:
Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 104, а площадь полной поверхности этой пирамиды равна 120. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
Дано: SABCD - правильная пирамида;
Sбок = 104; Sполн = 120.
Найти: S (ASC)
Решение:
- В основании правильной четырехугольной пирамиды лежит квадрат, а все боковые грани - равнобедренные треугольники.
Площадь боковой поверхности равна:
Sбок = 1/2 Рl,
где Р - периметр основания, l - апофема.
Площадь полной поверхности равна:
Sполн = Sосн + Sбок
⇒ Sосн = Sполн - Sбок
Sосн = 120 - 104 = 16
Площадь квадрата равна:
Sосн = а²,
где а - сторона квадрата.
⇒ AD = √16 = 4
Периметр квадрата равен:
Р = 4а
Р = 4 · 4 = 16
Проведем высоту SH. Соединим Н и О.
Найдем апофему SH из формулы Sбок:
104 = 1/2 · 16 · SH
SH = 13
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ DH = HC
Рассмотрим ΔACD - прямоугольный.
По теореме Пифагора:
АС² = AD² + DC² = 16 + 16 = 32 ⇒ AC = 4√2
- Диагонали квадрата точкой пересечения делятся пополам.
⇒ АО = ОС
DH = HC
⇒ ОН - средняя линия.
- Средняя линия равна половине стороны, которую она не пересекает.
⇒ ОН = AD : 2 = 2
Рассмотрим ΔОSH - прямоугольный.
По теореме Пифагора:
OS² = SH² - OH² = 169 - 4 = 165 ⇒ OS = √165
Рассмотрим ΔASC.
Площадь треугольника равна:
S = 1/2 · ah,
где а - сторона, h - высота, проведенная к этой стороне.
S(ASC) = 1/2 · AC · OS = 1/2 · 4√2 · √165 = 2√330
Площадь сечения равна 2√330 ед².
#SPJ1