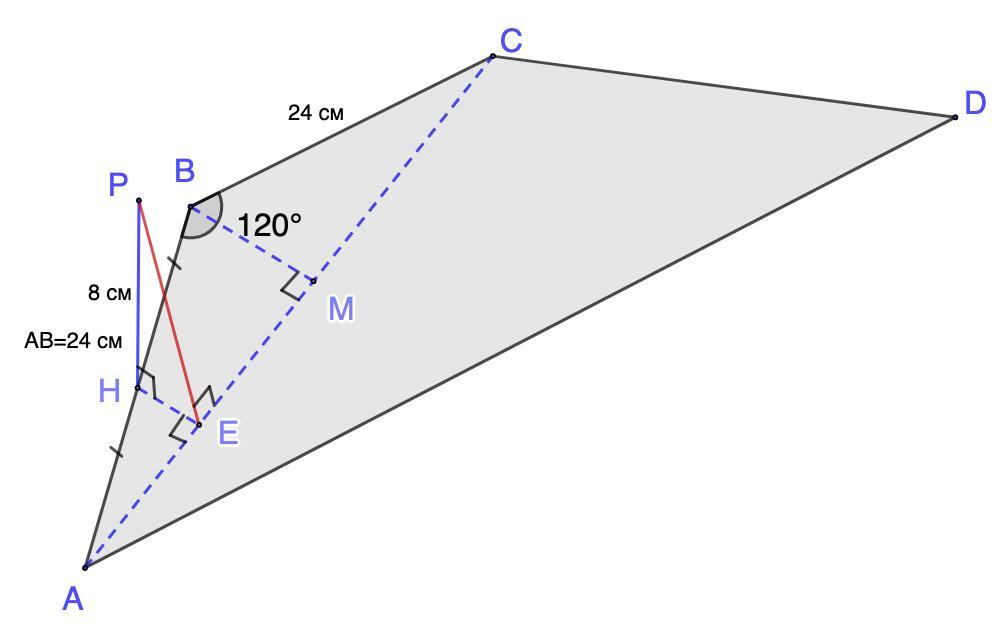
Із точки Н - середини бічної сторони АВ рівнобічної трапеції ABCD (ВС || AD) - до її площини проведено перпендикуляр НР, що дорівнює 8 см. Знайди відстань від точки Р до діагоналі АС, якщо AB = BC = 24cм /_ABC = 120° .
Ответы
Ответ:
Расстояние от точки Р до диагонали АС равно 10 см.
Объяснение:
Из точки Н - середины боковой стороны АВ равносторонней трапеции ABCD (ВС || AD) - к ее плоскости проведен перпендикуляр НР, равный 8 см. Найди расстояние от точки Р до диагонали АС, если AB = BC = 24 см, ∠ABC = 120°.
Дано: ABCD - равнобедренная трапеция;
НР ⊥ ABCD; AH = HB;
AB = BC = 24 cм;
∠ABC = 120°
Найти: расстояние от точки Р до диагонали АС
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ РЕ ⊥ АС, то есть искомый отрезок РЕ.
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ей самой, перпендикулярна и ее проекции.
⇒ НЕ ⊥ АС
Проведем ВМ ⊥ АС
Рассмотрим ΔАВС - равнобедренный ( AB = BC = 24 cм)
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
⇒ ∠АВМ = ∠МВС = 120° : 2 = 60°
Рассмотрим ΔАВМ - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ВАМ = 90° - 60° = 30°
- Катет, лежащий против угла 30° равен половине гипотенузы.
⇒ ВМ = АВ : 2 = 24 : 2 = 12 (см)
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ НЕ || BM
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
⇒ НЕ - средняя линия.
- Средняя линия равна половине стороны, которую она не пересекает.
⇒ НЕ = ВМ : 2 = 12 : 2 = 6 (см)
Рассмотрим ΔНРЕ - прямоугольный.
По теореме Пифагора:
РЕ² = РН² + НЕ² = 64 + 35 = 100 ⇒ РЕ = 10 см
#SPJ1