Предмет: Алгебра,
автор: Аноним
Найдите область определения функции, фото прикрепил
Приложения:
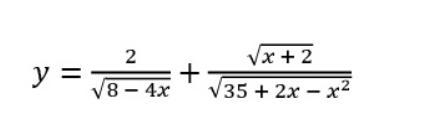
Ответы
Автор ответа:
0
Ответ:
Знаменатель дроби не может равняться 0 . Подкоренное выражение корня чётной степени должно быть неотрицательно .
P.S. Корни квадратного трёхчлена найдены по тtореме
Виета , поэтому возможно разложение
. Неравенство со знаком меньше даёт
интервал между корнями .
Приложения:

masha01021:
здравствуйте, еще помогите пожалуйста
Похожие вопросы
Предмет: Алгебра,
автор: kostuningleb04
Предмет: Математика,
автор: hiukdhdsk286
Предмет: Литература,
автор: kamad17
Предмет: Литература,
автор: alinaandrejeva2006
Предмет: История,
автор: Veravratova