Предмет: Геометрия,
автор: anastasiahodos32
Дві площини перетинаються під кутом 45°. Точка А належить одній з площин і віддалена від їх лінії перетину на 6 см. Знайдіть відстань від точки А до другої площини
(з поясненнями)
(якщо ви розумієте геометрію подивіться мої останні запитання)
Ответы
Автор ответа:
1
Автор ответа:
1
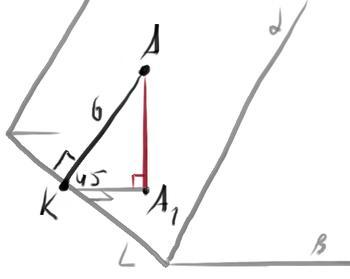
Плоскости a и b пересекаются по прямой L.
Точка A лежит в плоскости a.
Расстояние от точки до прямой - длина перпендикуляра.
Проведем AK⊥L, AK=6
Опустим AA1_b
Если прямая перпендикулярна наклонной, то она препендикулярна и проекции наклонной (т о трех перпендикулярах).
AA1⊥b, AK_L => A1K⊥L
Угол между плоскостями - угол между перпендикулярами к общей прямой.
∠(a;b) =∠AKA1 =45°
Тогда AA1 =AK sinAKA1 =6 sin45° =6 √2/2 =3√2 (см)
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: astalma2012
Предмет: Химия,
автор: h50166864
Предмет: Қазақ тiлi,
автор: alena132061
Предмет: Литература,
автор: inna011282
Предмет: Английский язык,
автор: nikolayfilipenko02
БЫЛО решение такой задачи. Поиск примени.