Помогите пожалуйста 100 баллов!!!
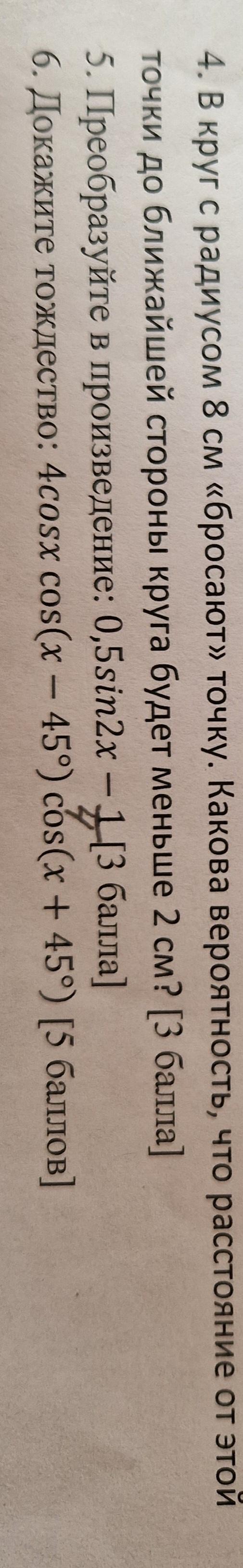
Ответы
4) Чтобы найти вероятность того, что расстояние от случайно выбранной точки внутри круга до ближайшей стороны круга будет меньше 2 см, можно использовать геометрический подход.
Рассмотрим круг с радиусом 8 см. Чтобы расстояние до ближайшей стороны круга было меньше 2 см, точка должна находиться внутри кольца с внутренним радиусом 6 см и внешним радиусом 10 см.
Площадь круга с радиусом 8 см равна π * (8 см)^2 = 64π см^2.
Площадь кольца с внутренним радиусом 6 см и внешним радиусом 10 см равна разности площадей двух кругов: π * (10 см)^2 - π * (6 см)^2 = 100π - 36π = 64π см^2.
Таким образом, вероятность того, что расстояние от случайно выбранной точки до ближайшей стороны круга будет меньше 2 см, равна площади кольца (64π см^2) поделенной на площадь всего круга (64π см^2):
Вероятность = (64π см^2) / (64π см^2) = 1.
Таким образом, вероятность равна 1, что расстояние от выбранной точки до ближайшей стороны круга будет меньше 2 см.
5) Для преобразования выражения в произведение, мы можем использовать формулу двойного угла для синуса.
Исходное выражение: 0,5sin2x - 11
Формула двойного угла для синуса:
sin2x = 2sinxcosx
Применяем формулу:
0,5sin2x - 11 = 0,5 * 2sinxcosx - 11 = sinxcosx - 11
Таким образом, исходное выражение 0,5sin2x - 11 может быть преобразовано в произведение sinxcosx - 11.
6) Для доказательства данного тождества, мы воспользуемся формулой двойного угла для косинуса и формулами сложения и вычитания углов для косинуса.
Исходное тождество: 4cosx cos(x - 45°) cos(x + 45°)
Формула двойного угла для косинуса:
cos2x = 2cos^2x - 1
Применяем формулу двойного угла:
4cosx cos(x - 45°) cos(x + 45°) = 2(2cosx cos(x - 45°) cos(x + 45°)) - 2
Теперь воспользуемся формулами сложения и вычитания углов для косинуса:
cos(A + B) = cosAcosB - sinAsinB
cos(A - B) = cosAcosB + sinAsinB
Применяем формулы к выражению в скобках:
2(2cosx cos(x - 45°) cos(x + 45°)) - 2
= 2(cosx(cos(x - 45°) + cos(x + 45°)) - sinx(sin(x - 45°) - sin(x + 45°))) - 2
= 2(cosxcosx - cosxsin45° + cosxcosx + cosxsin45°) - 2
= 2(2cos^2x) - 2
= 4cos^2x - 2.
Таким образом, исходное тождество 4cosx cos(x - 45°) cos(x + 45°) равно 4cos^2x - 2.
Ответ:4) Чтобы найти вероятность того, что расстояние от случайно выбранной точки внутри круга до ближайшей стороны круга будет меньше 2 см, можно использовать геометрический подход.
Рассмотрим круг с радиусом 8 см. Чтобы расстояние до ближайшей стороны круга было меньше 2 см, точка должна находиться внутри кольца с внутренним радиусом 6 см и внешним радиусом 10 см.
Площадь круга с радиусом 8 см равна π * (8 см)^2 = 64π см^2.
Площадь кольца с внутренним радиусом 6 см и внешним радиусом 10 см равна разности площадей двух кругов: π * (10 см)^2 - π * (6 см)^2 = 100π - 36π = 64π см^2.
Таким образом, вероятность того, что расстояние от случайно выбранной точки до ближайшей стороны круга будет меньше 2 см, равна площади кольца (64π см^2) поделенной на площадь всего круга (64π см^2):
Вероятность = (64π см^2) / (64π см^2) = 1.
Таким образом, вероятность равна 1, что расстояние от выбранной точки до ближайшей стороны круга будет меньше 2 см.
5) Для преобразования выражения в произведение, мы можем использовать формулу двойного угла для синуса.
Исходное выражение: 0,5sin2x - 11
Формула двойного угла для синуса:
sin2x = 2sinxcosx
Применяем формулу:
0,5sin2x - 11 = 0,5 * 2sinxcosx - 11 = sinxcosx - 11
Таким образом, исходное выражение 0,5sin2x - 11 может быть преобразовано в произведение sinxcosx - 11.
6) Для доказательства данного тождества, мы воспользуемся формулой двойного угла для косинуса и формулами сложения и вычитания углов для косинуса.
Исходное тождество: 4cosx cos(x - 45°) cos(x + 45°)
Формула двойного угла для косинуса:
cos2x = 2cos^2x - 1
Применяем формулу двойного угла:
4cosx cos(x - 45°) cos(x + 45°) = 2(2cosx cos(x - 45°) cos(x + 45°)) - 2
Теперь воспользуемся формулами сложения и вычитания углов для косинуса:
cos(A + B) = cosAcosB - sinAsinB
cos(A - B) = cosAcosB + sinAsinB
Применяем формулы к выражению в скобках:
2(2cosx cos(x - 45°) cos(x + 45°)) - 2
= 2(cosx(cos(x - 45°) + cos(x + 45°)) - sinx(sin(x - 45°) - sin(x + 45°))) - 2
= 2(cosxcosx - cosxsin45° + cosxcosx + cosxsin45°) - 2
= 2(2cos^2x) - 2
= 4cos^2x - 2.
Таким образом, исходное тождество 4cosx cos(x - 45°) cos(x + 45°) равно 4cos^2x - 2.
Объяснение: