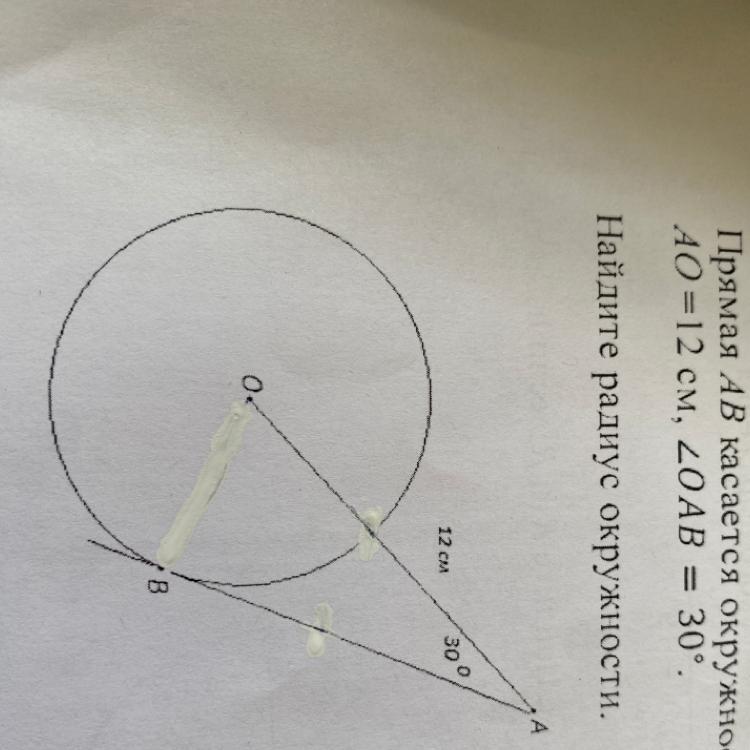
Прямая АВ касается окружности в точке В.
A0 = 12 cM, OAB = 30°.
наидите радиус окружности.
(То, что корректором замазала это я начеркала)
Ответы
Ответ:
Для розв'язання цієї задачі скористаємося властивостями трикутника, утвореного відрізками OA, OB та дугою AB окружності.
Оскільки пряма AB є дотичною до окружності в точці В, то кут OAB є прямим кутом (90°).
Також дано, що OA = 12 см.
Запишемо відому інформацію:
OA = 12 см
OAB = 90°
З умови задачі видно, що трікутник OAB є прямокутним з катетами OA і OB.
Використовуючи тригонометрію в прямокутному трикутнику OAB, можемо використати тангенс кута OAB, щоб знайти співвідношення між сторонами OA і OB.
tan(OAB) = OB/OA
Так як OAB = 90°, то тангенс 90° дорівнює нескінченності. Отже, співвідношення між сторонами OA і OB дорівнює нескінченності:
OB/OA = ∞
Це означає, що сторона OB нескінченно велика в порівнянні зі стороною OA. Отже, можемо вважати, що OB прямує до радіусу R окружності.
Таким чином, радіус R окружності є нескінченністю або можна сказати, що радіус окружності нескінченно великий