Предмет: Геометрия,
автор: 99UwU99
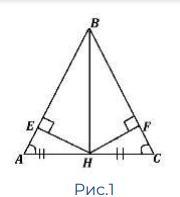
По данным рисунка 1 докажите
равенство треугольников BEH и BFH.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Доказано, что ΔBEH = ΔBFH
Объяснение:
Дано: АН=НС, ∠А=∠С, НЕ⊥АВ, HF⊥BC
Доказать: ΔBEH = ΔBFH
Доказательство
1) Рассмотрим ΔАЕН и ΔСFН
Так как НЕ⊥АВ, HF⊥BC, то они прямоугольные:
∠АЕН=∠СFН=90°
- АН=НС - по условию (гипотенузы равны),
- ∠А=∠С - по условию (острые углы равны).
Следовательно ΔАЕН = ΔСFН по гипотенузе и острому углу.
Из равенства треугольников следует равенство соответствующих сторон:
ЕН=FН
2) Рассмотрим ΔBEH и ΔBFH
Так как НЕ⊥АВ, HF⊥BC, то они прямоугольные:
∠BEH=∠BFH=90°
- ЕН=FН - пункт 1 (катеты равны)
- ВН - общая (гипотенуза для обоих треугольников)
ΔBEH = ΔBFH - по гипотенузе и катету, что и требовалось доказать.
#SPJ1
Похожие вопросы
Предмет: Українська мова,
автор: elvirabojko87
Предмет: Українська література,
автор: siridsadasha
Предмет: Литература,
автор: Аноним
Предмет: Русский язык,
автор: yarik124
Предмет: Математика,
автор: borodiivalerii