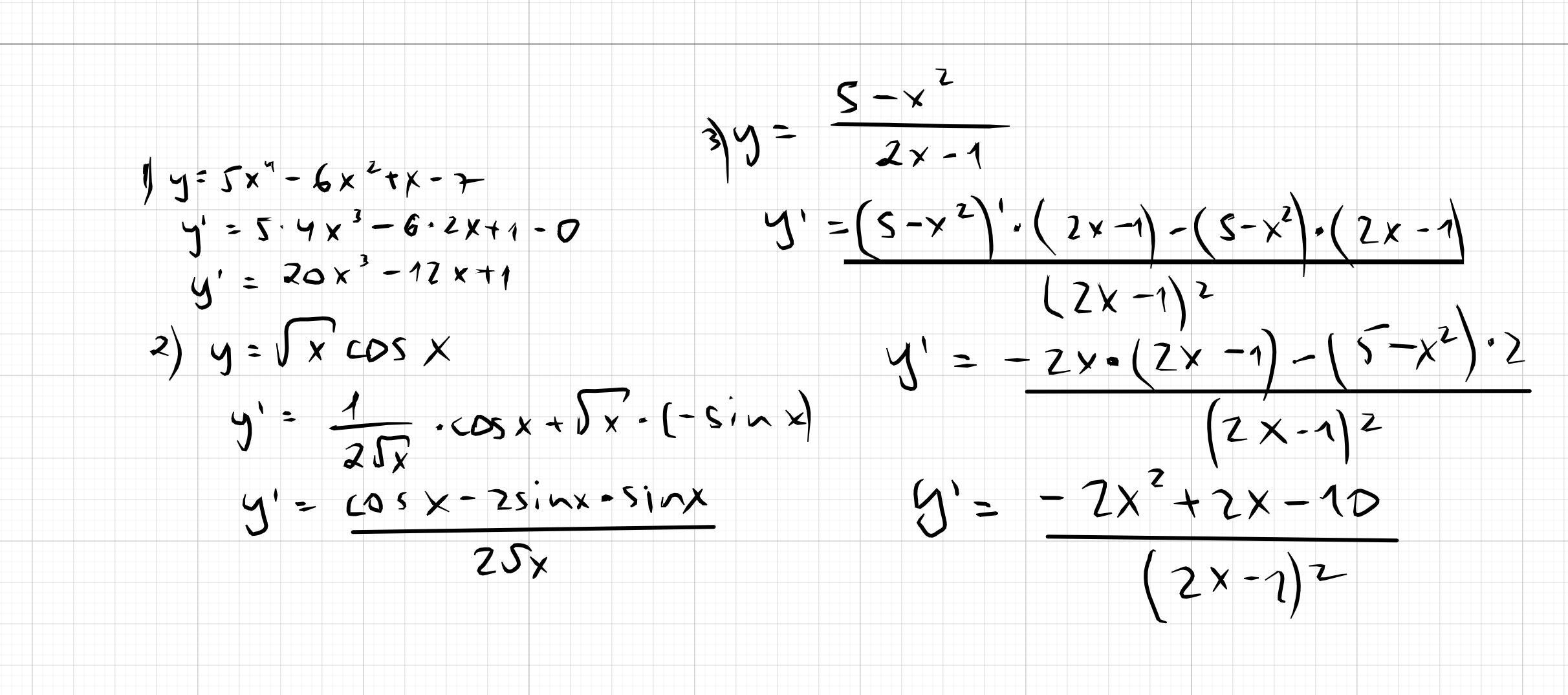. Обчисліть похідні функцій:
a) y = 5x ^ 4 - 6x ^ 2 + x - 7 b) y = √x cosx в) y = (5 - x ^ 2)/(2x - 1)
Ответы
Ответ:a) Для обчислення похідної функції y = 5x^4 - 6x^2 + x - 7, використаємо правила диференціювання степеневих функцій та констант:
y' = (5 * 4 * x^(4-1)) - (6 * 2 * x^(2-1)) + 1
= 20x^3 - 12x + 1
Отже, похідна функції y = 5x^4 - 6x^2 + x - 7 дорівнює 20x^3 - 12x + 1.
b) Для обчислення похідної функції y = √x * cos(x), використаємо правила диференціювання композиції функцій:
y' = (1/2) * (√x * cos(x)) + √x * (-sin(x))
= (1/2) * √x * cos(x) - √x * sin(x)
= (√x/2) * (cos(x) - 2sin(x))
Отже, похідна функції y = √x * cos(x) дорівнює (√x/2) * (cos(x) - 2sin(x)).
в) Для обчислення похідної функції y = (5 - x^2)/(2x - 1), використаємо правила диференціювання часткових дробів та ланцюжкового правила:
y' = ((2x - 1) * (-2x) - (5 - x^2) * 2) / (2x - 1)^2
= (-4x^2 + 2x + 10 - 2x^2) / (2x - 1)^2
= (-6x^2 + 2x + 10) / (2x - 1)^2
Отже, похідна функції y = (5 - x^2)/(2x - 1) дорівнює (-6x^2 + 2x + 10) / (2x - 1)^2.
Объяснение:
Ответ:
дай лучший ответ пж
Объяснение: