Предмет: Алгебра,
автор: sa0076773
СРОЧНО!! решите уравнение:
Приложения:
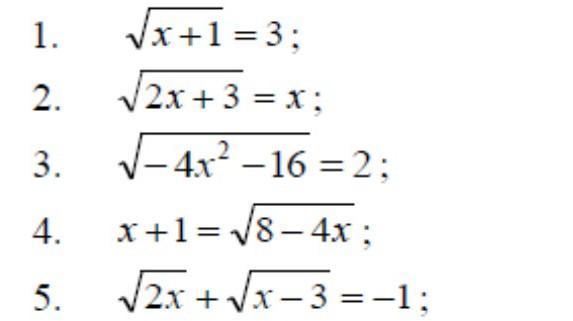
Ответы
Автор ответа:
1
Обяснение:
1.
ОДЗ: х+1≥0 х≥-1.
Ответ: х=8.
2.
ОДЗ:
Ответ: x=3.
3.
ОДЗ:
Ответ: уравнение не имеет решения.
4.
ОДЗ:
Ответ: х=1.
5.
Ответ: уравнение решения не имеет.
Похожие вопросы
Предмет: История,
автор: kamolovanigina46
Предмет: География,
автор: bezuglaamargo
Предмет: Українська мова,
автор: sporniktana
Предмет: Физика,
автор: vikka395
Предмет: Русский язык,
автор: Queen00900