Question

Мала діагональ ромба дорівнює 174 см, а периметр 580 см. Обчисліть площу ромба.

Answer 1

Ответ:

Площа ромба дорівнює 20184 см²

Пошаговое объяснение:

Мала діагональ ромба дорівнює 174 см, а периметр 580 см. Обчисліть площу ромба.

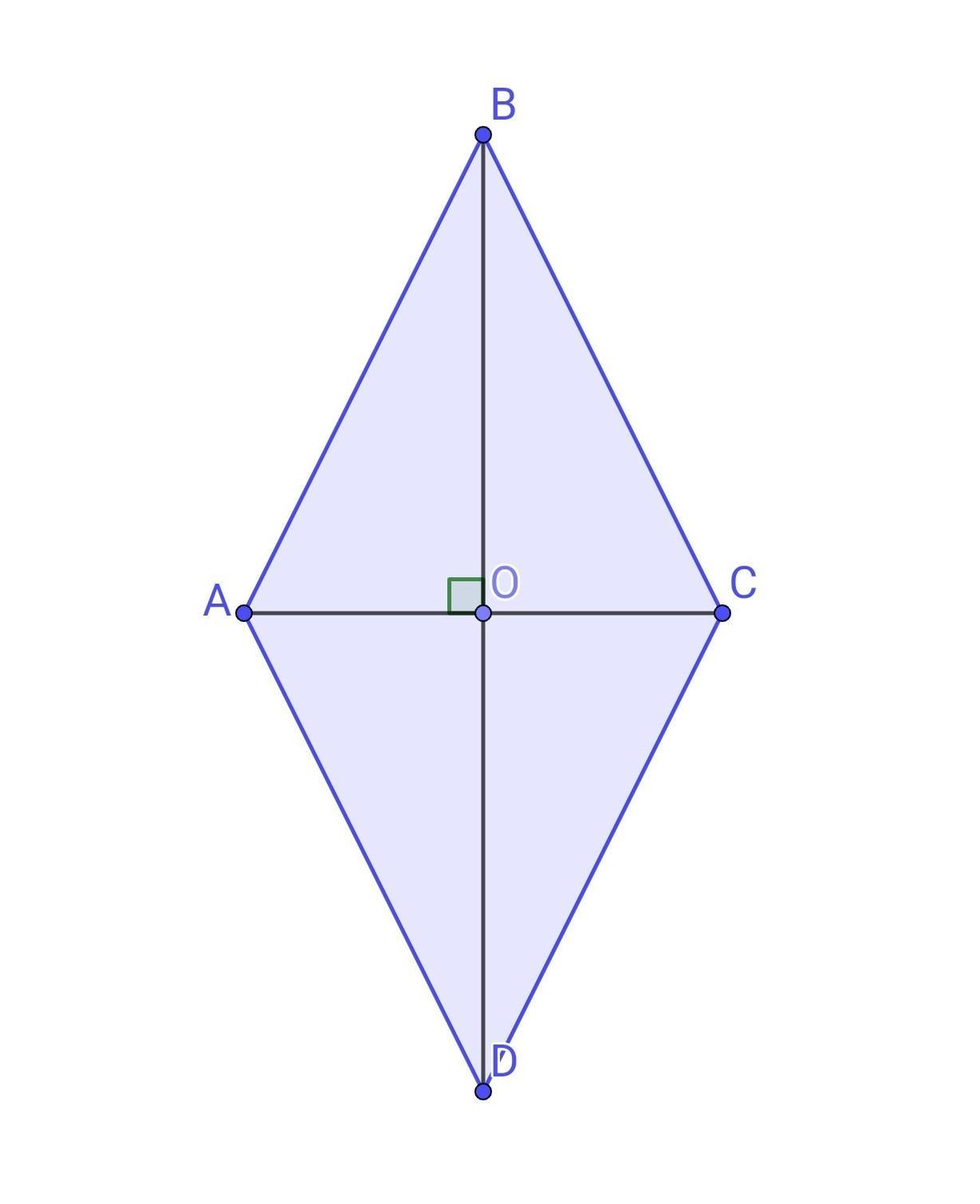
Нехай маємо ромб ABCD, AC= 174 см і BD - діагоналі ромба.

Р(ABCD) = 580 см.

Оскільки ромб - це паралелограм, у якого всі сторони рівні, то:

$AB = BC = CD = AD = \dfrac{1}{4} P_{ABCD} = \dfrac{580}{4} = \bf 145$ (см)

За властивістю паралелограма (діагоналі в точці перетину діляться навпіл):

AO=OC=½•AC=174/2=87(см).

Також BO=OD.

За властивістю ромба (діагоналі перетинаються під прямим кутом):

AC⟂BD, тому AO⟂BO, ⇒ ∠AOB=90°.

У прямокутному трикутнику AOB (∠AOB=90°) за теоремою Піфагора знайдемо катет ВО:

BO²=AB²-AO²

BO²=145²-87²=(145-87)(145+87)=58•232=2•29•29•8=29²•4²

BO=29•4= 116 (см)

Отже, діагональ BD = 2•BO = 2•116 = 232 (см)

Площа ромба дорівнює половині добутку його діагоналей:

$S = \dfrac{AC \times BD}{2} = \dfrac{174 \times 232}{2} = \bf 20184$ (см²)