Предмет: Алгебра,
автор: Dkdkdksske
даю 50 баллов
решите систему неравенств
x²-3x+9>0
x²<36
Приложения:
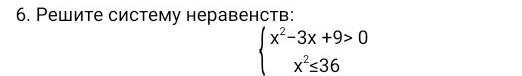
Ответы
Автор ответа:
0
Найдём корни квадратного трёхчлена , для этого приравняем его к нулю .
Дискриминант меньше нуля , значит корней нет .
Дискриминант меньше нуля , старший коэффициент больше нулю, значит x² - 3x + 9 > 0 при любых действительных значениях x , то есть решение этого неравенства : x ∈ ( - ∞ ; + ∞) .
Решим второе неравенство :
Похожие вопросы
Предмет: Математика,
автор: shiriaew52
Предмет: Литература,
автор: wwwowchik
Предмет: Алгебра,
автор: dp884930
Предмет: Химия,
автор: Davina24
Предмет: Математика,
автор: 380972589540