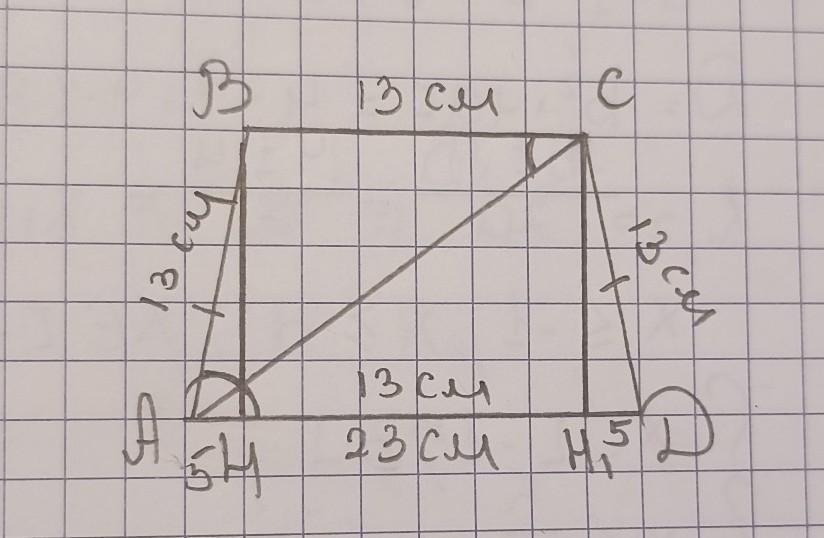
8. Основи рівнобічної трапеції дорівнюють 13 см і 23 см, а діагональ ділить її гострий кут
навпіл. Знайдіть площу трапеції.
СРОЧНО ДАЮ 100 балів!!!
Ответы
Ответ:
Рисунок в прикрепленном фото
Дано:
AD=23 см
BC=13 см
Найти:
S трапеции
Решение:
Проведём высоты BH и CH1. Мы получили прямоугольник BCHH1. Значит, сторона HH1=BC=13 см. AH=H1D, т. к. трапеция равнобокая. AH=H1D= (23-13)/2= 10/2=5
Угол A - острый; диагональ AC делит трапецию ABCD на два треугольника - ∆ABC и ∆ ACD. Угол А в ∆ ABC= Угол А в ∆ ACD, т. к. диагональ является биссектрисой.
Угол А в ∆ АСD= Угол C в ∆ ABC, как накрест лежащие углы при параллельных прямых.
Значит в ∆ABC угол А= угол С. Из этого: ∆АBC- равнобедренный, AB=BC= 13 см.
Т. к. трапеция равнобедренная, то AB=CD= 13 см
Рассмотрим прямоугольный ∆ ABH. По теореме Пифагора:
АН²+ВН²=АВ²
5²+ВН²=13²
25+ВН²=169
ВН²= 144
ВН= √144= 12 см
S трапеции= 1/2*(BC+AD)*h
S трапеции= 1/2*(13+23)*12= 1/2*36*12=216 см²
Ответ: S трапеции = 216 см²