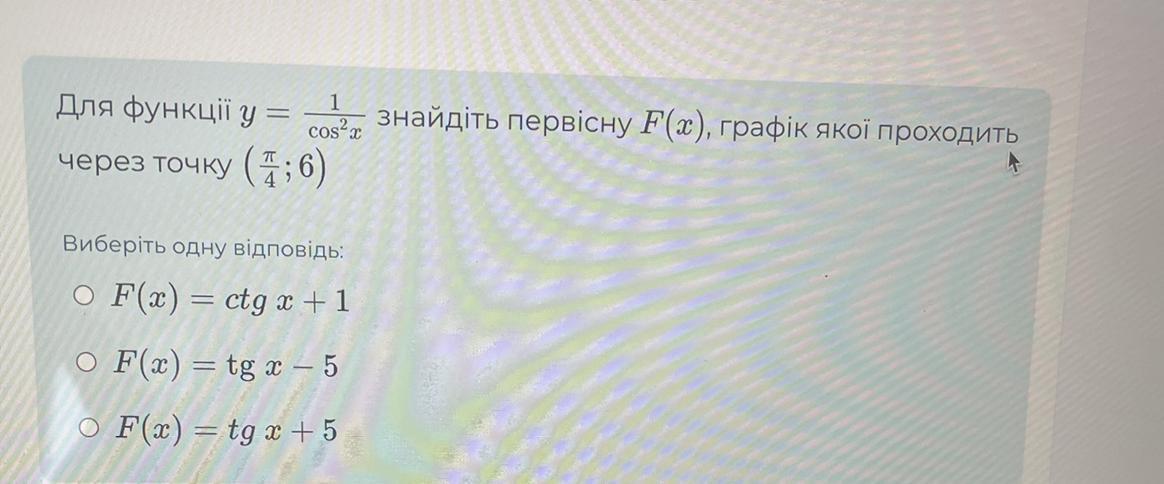
Для функції у = 1/cos^2x знайдіть первісну F(x), графік якої проходить через точку (π/4; 6)
Виберіть одну відповідь:
1. F(x) = ctg x + 1
2. F(x) = tg x — 5
3. F(x) = tg x + 45
Ответы
Ответ: 2
Щоб знайти первісну F(x) для функції у = 1/cos^2x та задовольнити умову, що графік первісної проходить через точку (π/4; 6), ми маємо обчислити неозначений інтеграл цієї функції та додати константу інтегрування, щоб врахувати початкову умову.
Інтегруємо функцію у = 1/cos^2x:
∫(1/cos^2x) dx
Ми можемо скористатися формулою заміни для інтегралу ∫(sec^2u) du = tan(u) + C:
∫(1/cos^2x) dx = ∫sec^2x dx = tan(x) + C
Додамо константу інтегрування C, щоб отримати загальний вигляд первісної F(x):
F(x) = tan(x) + C
Застосуємо початкову умову (π/4; 6):
F(π/4) = tan(π/4) + C = 1 + C
Оскільки точка (π/4; 6) лежить на графіку первісної, то значення F(π/4) повинно дорівнювати 6. Тому, 1 + C = 6.
C = 6 - 1
C = 5
Отже, первісна F(x) для функції у = 1/cos^2x з умовою, що графік проходить через точку (π/4; 6), має вигляд:
F(x) = tan(x) - 5