Предмет: Алгебра,
автор: folot1789
Используя признак лейбница исследуйте сходимость знакочередующегося ряда
Приложения:
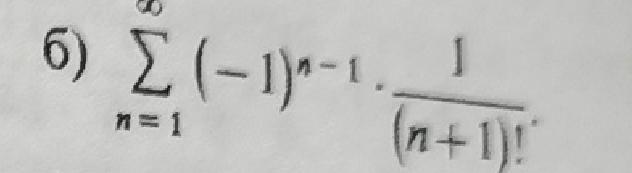
Ответы
Автор ответа:
2
Ответ:
Знакочередующийся ряд :
Проверим выполнение условий признака Лейбница .
выполняется
выполняется
Знакочередующийся ряд сходится по признаку Лейбница .
Ряд из абсолютных величин сходится по
признаку Даламбера , так как
Знакочередующийся ряд сходится абсолютно .
Приложения:

folot1789:
Спасибо
Еще один вопрос у меня в профиле
уже написала
Похожие вопросы
Предмет: Математика,
автор: nosenkokseniia
Предмет: Физика,
автор: deniskrutou46
Предмет: Русский язык,
автор: lavrivaleksandr85
Предмет: Математика,
автор: rubikorsikov
Предмет: Алгебра,
автор: inpruvd