Предмет: Математика,
автор: g02526750
Знайти інтеграли, використовуючи метод інтегрування частинами.
Приложения:
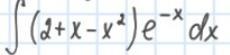
Ответы
Автор ответа:
0
Решение.
В этом примере придётся два раза применять интегрирование по частям, так как записан многочлен второй степени .
Формула : .
Приложения:
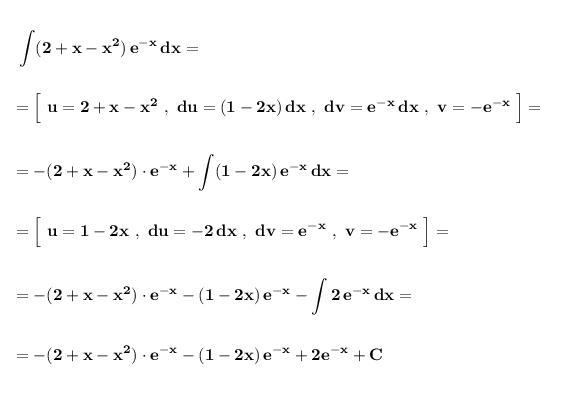
Похожие вопросы
Предмет: Физика,
автор: pdi1111111111
Предмет: Українська література,
автор: aedpekl
Предмет: Биология,
автор: berladin03
Предмет: Алгебра,
автор: sofiakuterhin
Предмет: Английский язык,
автор: zarylbekovna