Предмет: Геометрия,
автор: RyanGosling123
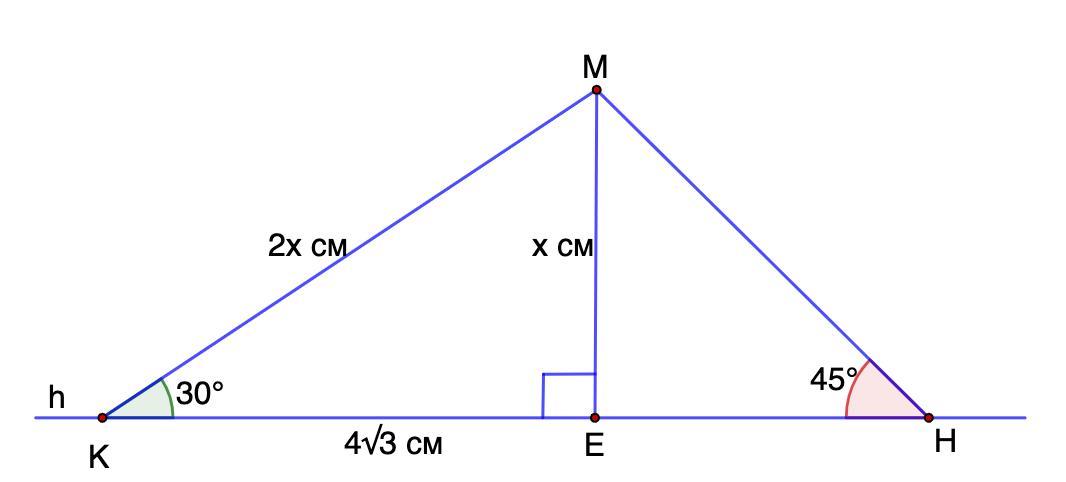
Із точки М, що лежить поза прямою h, проведено до цієї прямої похилі МК і МН, які утворюють з нею кути 30° і 45° відповідно. Знайдіть довжину похилої МН, якщо довжина проекції похилої МК на пряму в дорівнює 4√3 см.
ДАЮ 100 Б. НАРИСУЙТЕ РИСУНОК, И УСЛОВИЯ ЗАДАЧИ С РЕШЕНИЕМ
Ответы
Автор ответа:
2
Ответ:
Длина наклонной МН равна 4√2 см.
Объяснение:
Из точки М, лежащей вне прямой h, проведены к этой прямой наклонные МК и МН, которые образуют с ней углы 30° и 45° соответственно. Найдите длину наклонной МН, если длина проекции наклонной МК на прямую равна 4√3 см.
Дано: h - прямая;
МК и МН - наклонные;
МЕ ⊥ h.
КЕ = 4√3 см; ∠МКЕ = 30°; ∠МНЕ = 45°.
Найти: МН
Решение:
1. Рассмотрим ΔКМЕ - прямоугольный.
МКЕ = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
Пусть МЕ = х см, тогда МК = 2х см.
По теореме Пифагора:
- Квадрат гипотенузы равен сумме квадратов катетов.
КМ² = КЕ² + МЕ²
4х² = 48 + х²
3х² = 48 |:3
x² = 16
x = 4
⇒ МЕ = 4 см
2. Рассмотрим ΔЕМН - прямоугольный.
∠МНЕ = 45°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ЕМН = 90° - ∠МНЕ = 90° - 45° = 45°
- Если в треугольнике два угла равны, то он равнобедренный.
⇒ МЕ = ЕН = 4 см
По теореме Пифагора:
МН² = МЕ² + ЕН² = 16 + 16 = 32 ⇒ МН = √32 = 4√2 (см)
Длина наклонной МН равна 4√2 см.
Приложения:
RyanGosling123:
спасибо вам)
Яка з даних послідовностей є геометричною прогресією?
а) 1; 4; 16; 64....
б) 12; 9; 6; 3....
в) 1; 3; 6; 9....
г) -10; -8; -6....
а) 1; 4; 16; 64....
б) 12; 9; 6; 3....
в) 1; 3; 6; 9....
г) -10; -8; -6....
Помогите пожалуйста
Похожие вопросы
Предмет: Физика,
автор: lsbpts
Предмет: История,
автор: musichouselove1
Предмет: Биология,
автор: sniganapolishuk2010
Предмет: Математика,
автор: rusdingo63
Предмет: Математика,
автор: SamatovRayimjan