Предмет: Математика,
автор: fishgrave
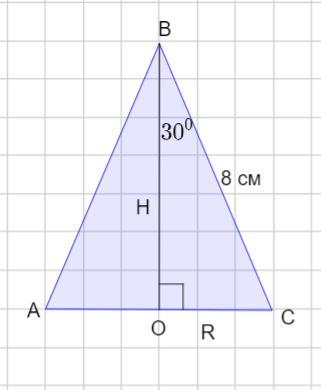
Твірна конуса дорівнює 8 см і утворює з висотою кут 30°. Знайдіть висоту конуса та його радіус.(з малюнком)
Ответы
Автор ответа:
1
Ответ:
R =4 cм, Н = 4√3 см.
Пошаговое объяснение:
Образующая конуса равно 8 см и образует с высотой угол 30°. Найти высоту конуса и его радиус.
ΔАВС - осевое сечение конуса. ΔАВС - равнобедренный ,
АВ =ВС = 8 см. ВО - высота конуса, ОС - радиус. ∠ СВО =30°.
ΔСВО - прямоугольный
В прямоугольном треугольнике напротив угла в 30° лежит катет, равный половине гипотенузы.
ОС = 8: 2 = 4 см.
Тогда радиус основания конуса R =4 cм.
Найдем высоту конуса, применив теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
ВС² = ВО² +ОС²;
ВО² = ВС² - ОС²;
ВО² = 8² - 4² = 64 - 16 = 48
ВО = √48 = 4√3.
Тогда высота конуса Н = 4√3 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: История,
автор: valentinalitvin82
Предмет: Українська мова,
автор: lizapakhoda
Предмет: Физика,
автор: darya260400
Предмет: Алгебра,
автор: laren45
Предмет: Алгебра,
автор: nikitasulima