5. Решите систему уравнений: 2(x-y)+1=3x-4y 10-4(x+y)=3y-3x [4]
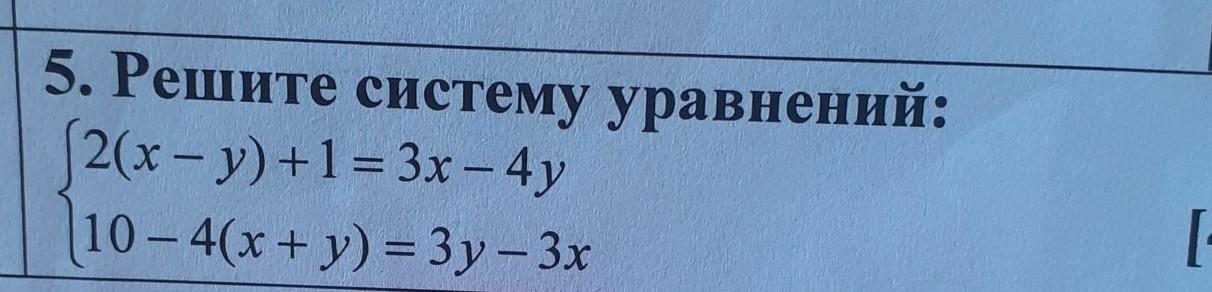
Ответы
Відповідь:
Давайте розв'яжемо дану систему уравнень:
2(x - y) + 1 = 3x - 4y
10 - 4(x + y) = 3y - 3x
Почнемо з другого рівняння. Розкриємо дужки:
10 - 4x - 4y = 3y - 3x
Тепер перегрупуємо подібні члени:
-4x + 3x - 4y - 3y = 10
-1x - 7y = 10 (рівняння 3)
Перепишемо перше рівняння:
2x - 2y + 1 = 3x - 4y
Також перегрупуємо подібні члени:
2x - 3x - 2y + 4y = -1
-x + 2y = -1 (рівняння 4)
Тепер ми маємо систему рівнянь:
-1x - 7y = 10
-x + 2y = -1
Ми можемо використати метод елімінації, щоб вирішити цю систему. Помножимо рівняння 4 на (-7):
7(-x + 2y) = 7(-1)
-7x + 14y = -7 (рівняння 5)
Тепер додамо рівняння 3 і рівняння 5, щоб елімінувати змінну "x":
(-1x - 7y) + (-7x + 14y) = 10 + (-7)
-8x + 7y = 3 (рівняння 6)
Тепер у нас є система двох рівнянь:
-8x + 7y = 3
-1x - 7y = 10
Додамо рівняння 6 і рівняння 2:
(-8x + 7y) + (10 - 4x - 4y) = 3 + 4
-12x - y + 10 = 7 (рівняння 7)
Розпишемо рівняння 7:
-12x - y + 10 = 7
Перенесемо 10 на другу сторону:
-12x - y = 7 - 10
-12x - y = -3 (рівняння 8)
Тепер ми маємо систему двох рівнянь:
-8x + 7y = 3
-12x - y = -3
Ми можемо використати метод елімінації, щоб вирішити цю систему. Помножимо рівняння 8 на 7:
7(-12x - y) = 7(-3)
-84x - 7y = -21 (рівняння 9)
Тепер додамо рівняння 9 і рівняння 1, щоб елімінувати змінну "y":
(-84x - 7y) + (2x - 2y + 1) = -21 + 1
-82x - 9y = -20 (рівняння 10)
Тепер ми маємо систему двох рівнянь:
-82x - 9y = -20
-8x + 7y = 3
Ми можемо використати метод елімінації, щоб вирішити цю систему. Помножимо рівняння 10 на 7 і рівняння 2 на 9:
7(-82x - 9y) = 7(-20)
9(-8x + 7y) = 9(3)
-574x - 63y = -140
-72x + 63y = 27
Тепер додамо рівняння 11 і рівняння 12, щоб елімінувати змінну "y":
(-574x - 63y) + (-72x + 63y) = -140 + 27
-646x = -113
Поділимо обидві сторони на -646:
x = (-113) / (-646)
x ≈ 0.175
Тепер підставимо значення x в рівняння 2, щоб знайти y:
10 - 4(0.175 + y) = 3y - 3(0.175)
10 - 0.7 - 4y = 3y - 0.525
-0.7 - 10 + 0.525 = 3y + 4y
-10.175 ≈ 7y
y = (-10.175) / 7
y ≈ -1.454
Таким чином, розв'язок системи уравнень буде:
x ≈ 0.175
y ≈ -1.454