Предмет: Геометрия,
автор: paradisesrandgame1
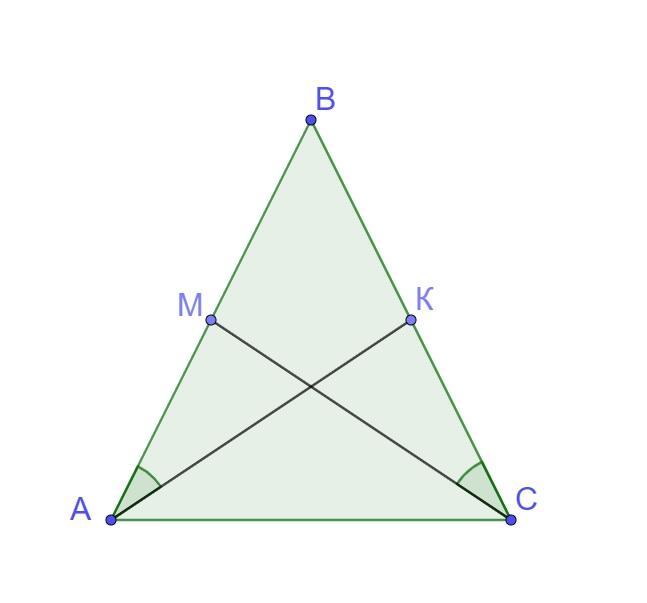
На бічних сторонах AB і BC рівнобедреного трикутника ABC позначили відповідно точки М і К так, що < BAK = <ВСМ. Доведіть, що ВМ=ВК
Ответы
Автор ответа:
2
Ответ:
Доведено, що ВМ=ВК
Объяснение:
На бічних сторонах AB і BC рівнобедреного трикутника ABC позначили відповідно точки М і К так, що ∠BAK = ∠ВСМ. Доведіть, що ВМ=ВК
За умовою ΔАВС - рівнобедрений, тому за означенням рівнобедреного трикутника AB = BC (як бічни сторони)
Розглянемо ΔАВК і ΔСВМ.
- АВ=ВС - як бічні сторони рівнобедреного ΔАВС
- ∠BAK = ∠ВСМ - за умовою
- ∠В - спільний
Тому ΔАВК=ΔСВМ за другою ознакою рівності трикутників (за стороною і двома прилеглими кутами)
З рівності трикутників випливає рівность відповідних сторін:
ВМ=ВК, що и треба було довести.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: natusy1801p6q0cm
Предмет: География,
автор: akmarzanbatken387
Предмет: Химия,
автор: nastalykanova38
Предмет: География,
автор: Zefirka87951
Предмет: Русский язык,
автор: Andrey20066