Question

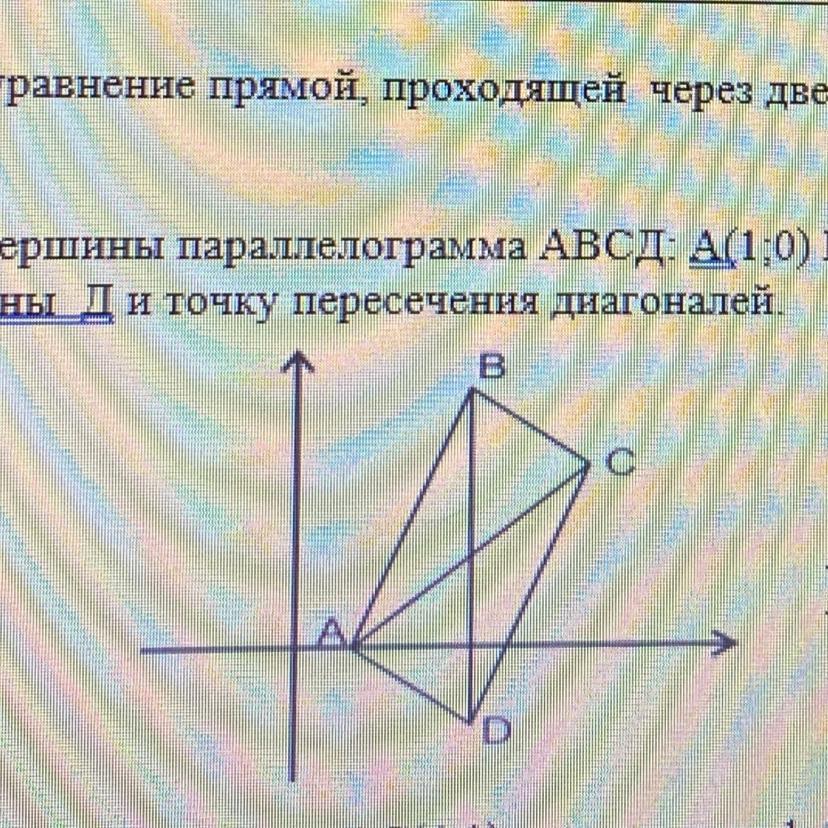
Даны три вершины параллелограмма АВСД: А(1:0) B(2:3) C(3:2). Найдите коорди-
наты вершины Д и точку пересечения
диагоналей.

Answer 1

Ответ:

Чтобы найти координаты вершины D параллелограмма, можно использовать свойство параллелограмма, согласно которому противоположные стороны параллелограмма равны и параллельны.

Мы знаем, что сторона AB параллельна стороне CD и равна ей. Поэтому мы можем найти координаты вершины D, прибавив к координатам точки C разность координат точек A и B:

D(x, y) = C(x, y) + (A(x, y) - B(x, y))

Для данного примера:

D(x, y) = C(3, 2) + (A(1, 0) - B(2, 3))

D(x, y) = (3, 2) + (-1, -3)

D(x, y) = (3 - 1, 2 - 3)

D(x, y) = (2, -1)

Таким образом, координаты вершины D параллелограмма равны (2, -1).

Чтобы найти точку пересечения диагоналей параллелограмма, мы можем найти среднюю точку между точками A и C.

Точка пересечения диагоналей будет иметь координаты, которые являются средними значениями соответствующих координат точек A и C:

X-координата точки пересечения диагоналей = (X-координата точки A + X-координата точки C) / 2

Y-координата точки пересечения диагоналей = (Y-координата точки A + Y-координата точки C) / 2

Для данного примера:

X-координата точки пересечения диагоналей = (1 + 3) / 2 = 2

Y-координата точки пересечения диагоналей = (0 + 2) / 2 = 1

Таким образом, координаты точки пересечения диагоналей параллелограмма равны (2, 1).