Question

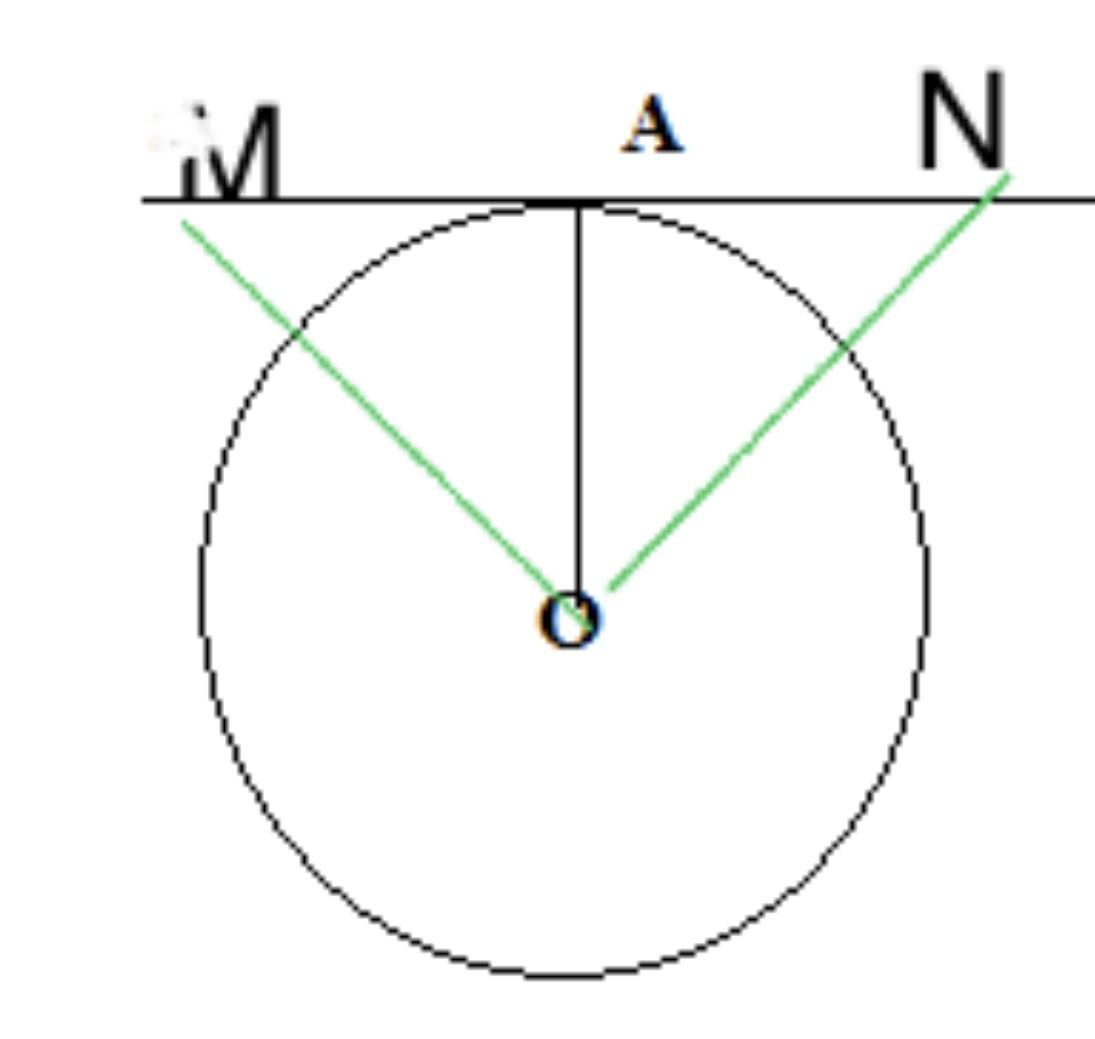
Пряма в точці А дотикається до кола із центром О. На дотичній по різні боки від точки А відкладено рівні відрізки АМ і АN. Доведіть, що ОМ=ON

Answer 1

Відповідь:

Пояснення:

Дано: 

О - центр кола; 

 А - точка дотику;  

АМ = АN  

Довести: ОМ = ОN

Доведення:

Проведемо радіус ОА. Радіус кола, проведений через точку дотику, перпендикулярний дотичній прямій. Звідси, ∠OAM = ∠OAN= 90*

.Розглянемо прямокутні трикутники АОМ і АОN.
AM = AN за умовою, АО - спільна сторона. 

Якщо катети одного прямокутного трикутника дорівнюють відповідно катетам другого, то такі трикутники рівні.Отже трикутники АОМ і АОN рівні.
З рівності трикутників випливає: ОМ = ОN.

Доведено.