Question

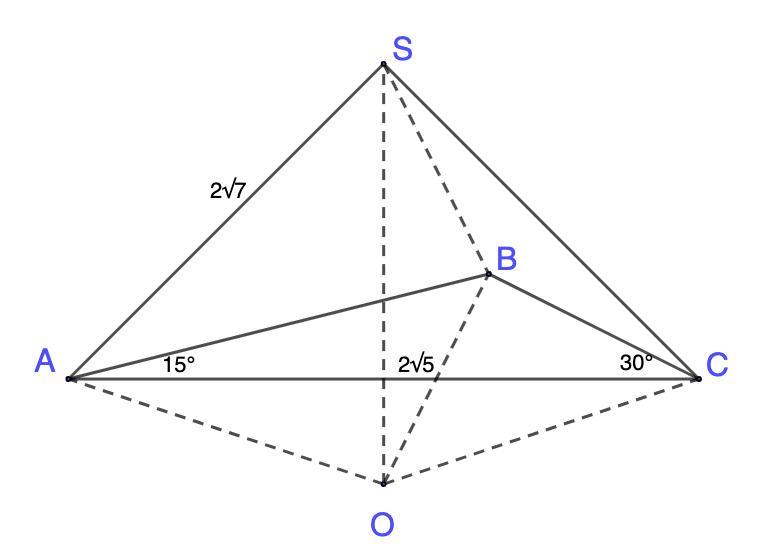
Основанием треугольной пирамиды SABC является Треугольник ABC. у которого ZBAC =15°, ZACB = 30°, АС=2√5. Каждое боковое ребро пирамиды SABC равно 2√7. Найдите значение выражения (√2 + √6) V, где и - объем пирамиды SABC.

Answer 1

Ответ:

Значение выражения (√2 + √6) V равно 10.

Объяснение:

Основанием треугольной пирамиды SABC является треугольник ABC. у которого ∠BAC = 15°, ∠ACB = 30°, АС=2√5. Каждое боковое ребро пирамиды SABC равно 2√7. Найдите значение выражения (√2 + √6) V, где V - объем пирамиды SABC.

Дано: SABC - пирамида.

ΔАВС - основание;

∠BAC = 15°, ∠ACB = 30°, АС=2√5.

SA = SB = SC = 2√7

Найти: (√2 + √6)V, где V - объем пирамиды SABC.

Решение:

• Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.

Рассмотрим ΔАВС.

• Сумма углов треугольника равна 180°.

⇒ ∠ АВС = 180° - 15° - 30° = 135°

• Стороны треугольника пропорциональны синусам противолежащих углов.

$\displaystyle \frac{AC}{sin135^0}=\frac{AB}{sin30^0}$

sin 135° = sin (180° - 45°) = sin 45° =√2/2;   sin 30° = 1/2.

$\displaystyle AB = \frac{2\sqrt{5} \cdot2}{2\cdot\sqrt{2} } =\sqrt{10}$

• Найдем площадь основания по формуле:

              S = 1/2 · ab ·sinα,

где а и b - стороны треугольника, α - угол между ними.

АВ = √10; АС = 2√5

sin 15° = sin (60° - 45°) = sin 60°cos 45° - cos 60°sin 45° =

$\displaystyle =\frac{\sqrt{3} }{2}\cdot \frac{\sqrt{2} }{2}-\frac{1}{2}\cdot\frac{\sqrt{2} }{2}=\frac{\sqrt{6}-\sqrt{2} }{4}$

$\displaystyle S=\frac{1}{2}\cdot \sqrt{10}\cdot 2\sqrt{5} \cdot \frac{\sqrt{6}-\sqrt{2} }{4} =5\sqrt{2} \cdot \frac{\sqrt{6}-\sqrt{2} }{4}$

Площадь основания нашли. Надо найти высоту пирамиды.

• Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной около треугольника окружности.

$\displaystyle \frac{AC}{sin 135^0}=2R\\ \\\frac{2\sqrt{5}\cdot 2 }{\sqrt{2} } =2R\;\;\;\Rightarrow \;\;\;R=\frac{2\sqrt{5} }{\sqrt{2} } =\sqrt{10}$

Рассмотрим ΔASO - прямоугольный.

По теореме Пифагора:

SO² = AS² - AO² = 28 - 10 = 18   ⇒   SO = 3√2

• Объем пирамиды равен:

      V = 1/3 · Sосн · h

$\displaystyle V=\frac{1}{3}\cdot 5\sqrt{2}\cdot\frac{\sqrt{6}-\sqrt{2} }{4}\cdot3\sqrt{2}=\frac{5}{2}(\sqrt{6}-\sqrt{2})$

Можем найти  (√2 + √6)V:

$\displaystyle \frac{5}{2}(\sqrt{6}-\sqrt{2})\cdot(\sqrt{6}+\sqrt{2})=\frac{5}{2}\cdot4=10$

Значение выражения (√2 + √6) V равно 10.

#SPJ1