Предмет: Геометрия,
автор: vetersleva
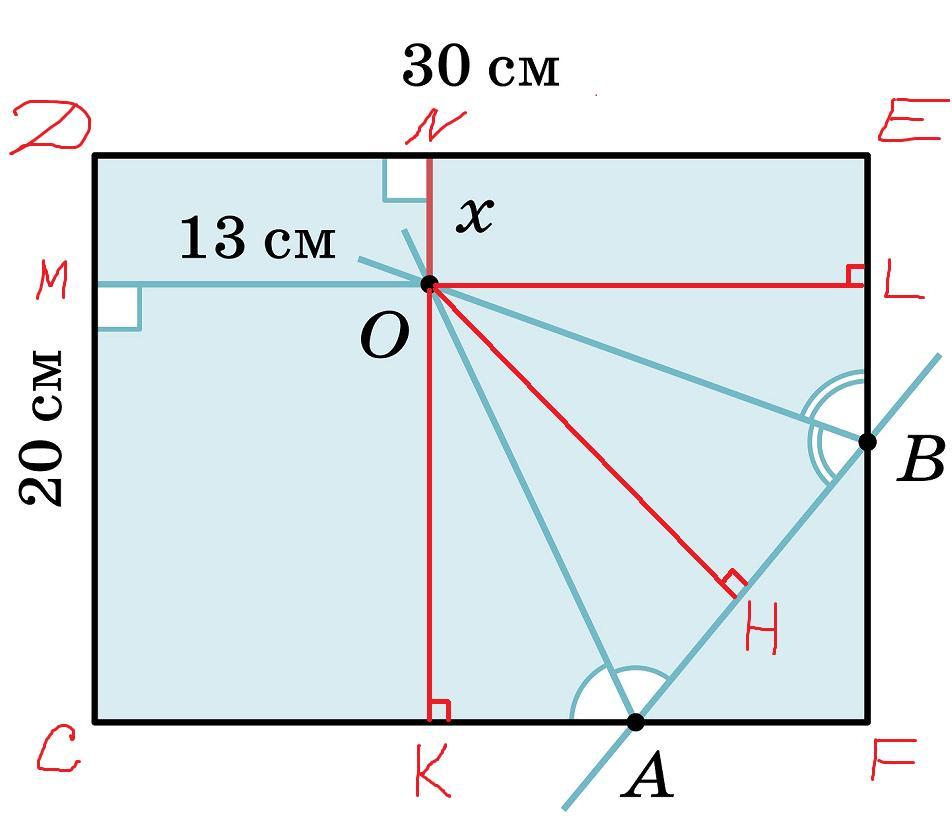
Прямая пересекает стороны прямоугольника с длинами 20 и 30 см в точках A и B. Биссектрисы тупых углов между ней и данными сторонами пересекаются в точке O, расстояние от которой до меньшей его стороны равно 13 см. Чему равно расстояние (в см) от точки O до большей стороны?
Приложения:

Ответы
Автор ответа:
2
Рассмотрим прямоугольник CDEF.
Рассмотрим угол CAB и биссектрису AO этого угла.
- Свойство биссектрисы: Любая точка, лежащая на биссектрисе, равноудалена от сторон угла.
Точка О лежит на биссектрисе AO угла CAB, следовательно точка O равноудалена от сторон этого угла: AC и AB. Расстоянием от точки до прямой является перпендикуляр:
Аналогично рассмотрим угол EBA и биссектрису BO этого угла.
Точка О лежит на биссектрисе BO угла EBA, следовательно точка O равноудалена от сторон этого угла: BE и BA:
Так как ОK=OH и ОL=OH, то ОK=ОL.
По построению:
CD || KN || EF и CF || ML || DE
Тогда:
OL = ML - MO = DE - MO
⇒ OL = 30 см - 13 см = 17 см
OK = OL
⇒ OK = 17 см
x = NK - OK = CD - OK
⇒ x = 20 см - 17 см = 3 см
Ответ: 3 см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: rimart012345
Предмет: История,
автор: elvirabojko87
Предмет: Математика,
автор: romashka3361861
Предмет: Английский язык,
автор: strelka3452
Предмет: Другие предметы,
автор: Аноним