ДАМ 35 БАЛЛОВ ЗА ЗАДАЧУ ПО ФИЗИКЕ (с решением и дано)
Какую площадь поперечного сечения имеет свинцовая проволока длиной 2м, в
которой при напряжении 12 В сила тока равна 0,4 А? Удельное сопротивление свинца (прикреплено в виде фотографии)
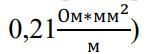
Ответы
Дано:
Длина проволоки (L) = 2 м
Напряжение (V) = 12 В
Сила тока (I) = 0,4 А
Удельное сопротивление свинца (ρ) = 0,21 μΩ·мм²/м
Для вычисления площади поперечного сечения (A) проволоки, мы можем использовать закон Ома:
V = I * R
Удельное сопротивление свинца (ρ) может быть выражено через сопротивление (R) и площадь поперечного сечения (A) следующим образом:
R = ρ * (L / A)
Подставляя значения, получаем:
12 = 0,4 * (0,21 * (2 / A))
Далее, решим уравнение относительно площади поперечного сечения (A):
12 = 0,4 * (0,42 / A)
12 = 0,084 / A
A = 0,084 / 12
A = 0,007 мм²
Таким образом, площадь поперечного сечения свинцовой проволоки составляет 0,007 мм².
Для решения этой задачи, мы можем использовать закон Ома, который гласит:
V = I* R,
V = 12 В I = 0,4 А.
Мы ищем площадь поперечного сечения проводника, поэтому нам нужно переупорядочить формулу:
A = (ρ * L) / R.
Подставим известные значения в формулу:
A = (0,21 ом мм2/м * 2 м) / R.
Теперь нам нужно найти сопротивление R. Воспользуемся законом Ома:
R = V / I = 12 В / 0,4 А = 30 ом.
Теперь подставим это значение в формулу для площади поперечного сечения:
A = (0,21 ом мм2/м * 2 м) / 30 ом.
A = 0,14 мм2.
Площадь поперечного сечения свинцовой проволоки 0,14 мм2.