Предмет: Алгебра,
автор: alice12324
Помогите пожалуйста решить. Ко второму заданию фото снизу прилагается.
1) Найдите наименьший положительный корень уравнения
cos x/6=1
2) Среди приведенных укажите уравнение, не имеющее корней на множестве действительных чисел.
3) Найдите количество корней уравнения 2 sin^2x-cos x=1 на промежутке [0; П].
Приложения:
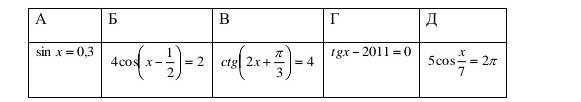
Ответы
Автор ответа:
1
Ответ:
1) Решить уравнение .
Наименьший положительный корень получим при n=1 , .
2) На множестве действительных чисел не имеет решений
уравнение Д , так как получаем значение функции косинус,
бОльшее 1 , а .
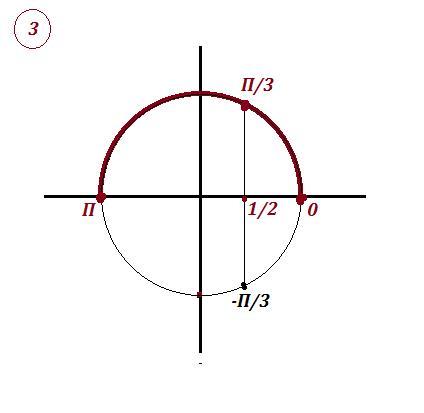
3) Уравнение : .
Из тригонометрической единицы выражаем функцию .
Переходим к старой переменной .
Три корня принадлежат заданному промежутку .
Ответ: три корня
принадлежат сегменту [ 0 ; π ] .
Приложения:

Похожие вопросы
Предмет: Қазақ тiлi,
автор: serikbajulyerasyl406
Предмет: Английский язык,
автор: larisacubera4
Предмет: Английский язык,
автор: Аноним
Предмет: Музыка,
автор: hofmani