Question

Вістань від точки перетину медіан трикутника АВС до сторони АВ дорівнює 10см. Знайти площу трикутника АВС,якщо АВ дорівнює 6см.

Answer 1

Ответ:

Площа трикутника АВС дорівнює 90 см²

Объяснение:

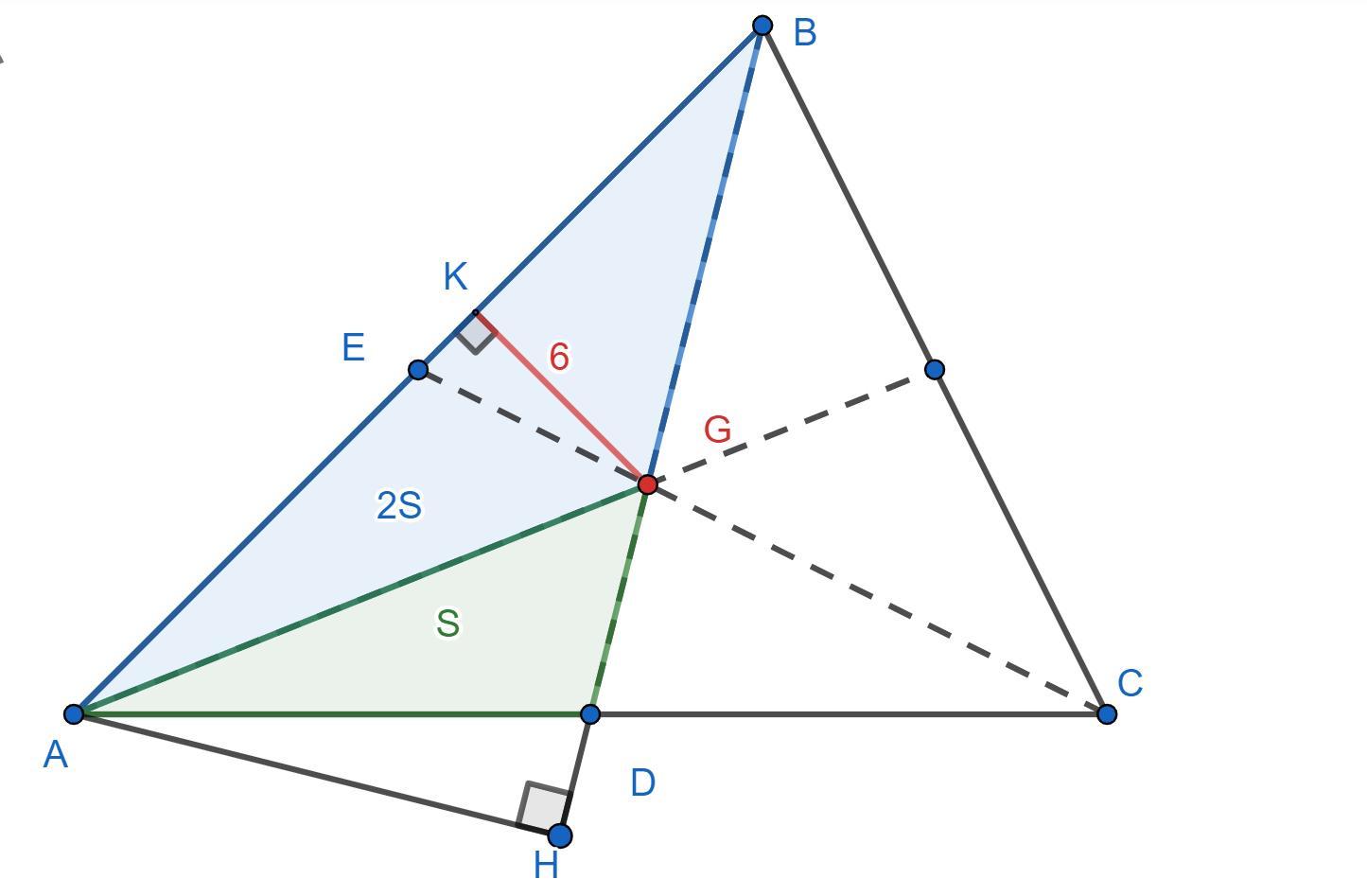
Пусть точка G , будет точкой пересечения медиан , опустим с данной точки на сторону  AB перпендикуляр  GK , длина которого по условию равна 10 см

Теперь мы можем найти площадь ΔABG , поскольку нам известно что AB = 6

$S_{ABG} = AB \cdot GK \cdot \dfrac{1}{2} = \dfrac{1}{2}\cdot 6 \cdot 10 = 30$  см²

Теперь вспомним , что медианы треугольника делят друг друга в отношении 2 : 1  считая от вершины треугольника

Соответственно  BG : GD = 2 : 1

Поскольку BG и  GD  являются частями основания BD ,  а  Δ-ки  ABG и  AGD имеют  общую высоту  AH ,  то отношение  площадей  Δ-ков  ABG и AGD  равно отношению их оснований  BG и  GD

$\dfrac{S_{ABG}}{S_{AGD}} = \dfrac{BG}{GD} = 2$

Подставим $S_{ABG} = 30$ см²

$\dfrac{30}{S_{AGD}} = 2 \\\\\\ S_{AGD} = 15$  см²

Таким образом   $S _{ABD} = S_{ABG} + S_{AGD} = 30 + 15 = 45$ см²

И в силу того , что  медиана  (BD)  делит треугольник (ABC) на два равных по площади треугольника ,  то  $S_{ABD} = S_{DBC}$  ⇒  площадь искомого  ΔABC  равна :

$S_{ABC}= S_{ABD} + S_{DBC} = 2 S_{ABD} = 2\cdot 45 = 90$  см²

#SPJ1