Предмет: Алгебра,
автор: nikita12131415161718
Срочно!!! Помогите пожалуйста
Приложения:
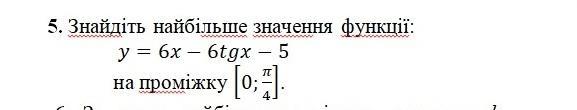
Ответы
Автор ответа:
2
Ответ:
- 5
Объяснение:
Найти наибольшее значение функции y= 6x - 6 tgx - 5 на промежутке [ 0; π/4] .
Найдем производную функции
Найдем критические точки, решив уравнение y'=0
Заданному промежутку [ 0; π/4] принадлежит х =0 (совпадает с концом промежутка) .
Найдем значения функции на концах промежутка
y(0) = 6 · 0 - 6 tg0 - 5 = 0 - 0 -5 = - 5;
y(π/4) = 6 · (π/4) - 6 tg(π/4) - 5 = 1,5 π - 6 · 1 -5 = 1,5π- 11.
Оценим полученное значение : π≈ 3,14; 1,5π≈ 4,71 и 4,71 - 11 = - 6,29.
Так как -6,29 < - 5 , то наибольшее значение функции равно - 5.
#SPJ1
Похожие вопросы
Предмет: Другие предметы,
автор: mashamariakuch
Предмет: Українська література,
автор: thepechenka16
Предмет: Алгебра,
автор: gena32358
Предмет: Математика,
автор: sergiy12314