дуже срочно даю 70б
зн екстремумів функції
y=3/4x⁴-4x³+6x²+1
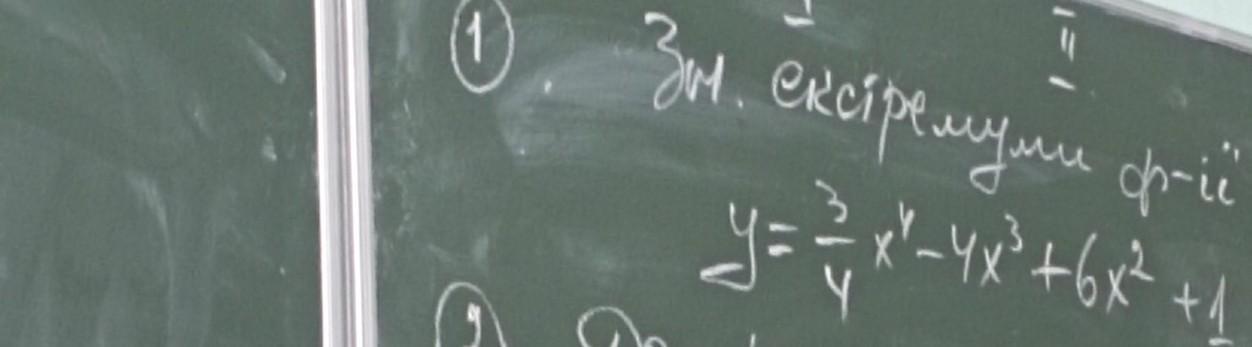
Ответы
Відповідь:Для знаходження екстремумів функції y = (3/4)x^4 - 4x^3 + 6x^2 + 1, спочатку візьмемо похідну функції і прирівняємо його до нуля, щоб знайти критичні точки:
y' = 4(3/4)x^3 - 3(4)x^2 + 2(6)x
= 3x^3 - 12x^2 + 12x
Далі, прирівняємо похідну до нуля:
3x^3 - 12x^2 + 12x = 0
Факторизуємо це рівняння:
3x(x^2 - 4x + 4) = 0
Отримуємо два фактори:
x = 0
x^2 - 4x + 4 = 0
Розв'язавши друге рівняння, отримуємо:
(x - 2)^2 = 0
x - 2 = 0
x = 2
Таким чином, маємо дві критичні точки: x = 0 та x = 2.
Для визначення типів екстремумів, ми повинні дослідити знак похідної в околі кожної критичної точки.
Для x = 0:
Підставимо значення x = 0 в похідну:
y'(0) = 3(0)^3 - 12(0)^2 + 12(0) = 0
Оскільки похідна дорівнює нулю, це може бути точка максимуму або мінімуму. Для визначення типу екстремуму, дослідимо знак другої похідної.
y'' = 6x - 24
Підставимо значення x = 0 в другу похідну:
y''(0) = 6(0) - 24 = -24
Оскільки друга похідна від'ємна, маємо точку максимуму при x = 0.
Для x = 2:
Підставимо значення x = 2 в похідну:
y'(2) = 3(2)^3 - 12(2)^2 + 12(2) = 24 - 48 + 24 = 0
Аналогічно, для визначення типу екстремуму, дослідимо знак другої похідної.
y''(2)
Пояснення: