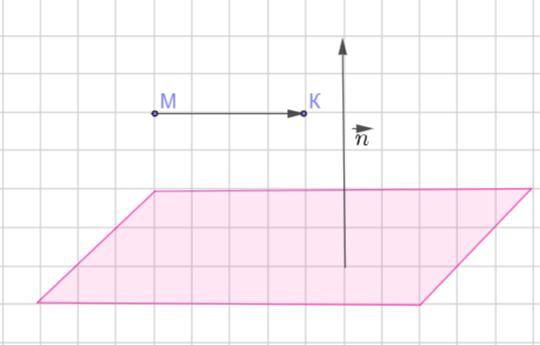
Дано точки М (3; a; -5) і К (7; 1; a). При якому значенні а, пряма МК паралельна площині 4x-3y+z-6=0?
Ответы
Ответ:
а = -4,5.
Объяснение:
Даны точки М( 3; а; - 5) и К ( 7; 1; а) . При каком значении а , прямая МК параллельна площади 4x - 3y +z - 6 =0 .
Рассмотрим плоскость 4x - 3y +z - 6 =0. Вектор - нормаль к плоскости имеет координаты (a; b; c) для плоскости ax + by + cz +d=0
Тогда вектор нормали к заданной плоскости
Рассмотрим направляющий вектор прямой МК вектор
И найдем его координаты. Для этого от координат конца вектора надо вычесть соответствующую координату начала вектора.
Если вектор параллелен плоскости, значит он перпендикулярен к вектору нормали, то есть ⊥
Воспользуемся условием перпендикулярности векторов: если векторы перпендикулярны, то их скалярное произведение равно нулю.
Скалярное произведение векторов равно сумме произведений одноименных координат.
Тогда 4а + 18=0;
4а = -18;
а = -18 : 4;
а= -4,5
Значит, при а = -4,5 прямая МК параллельна плоскости.
#SPJ1