Question

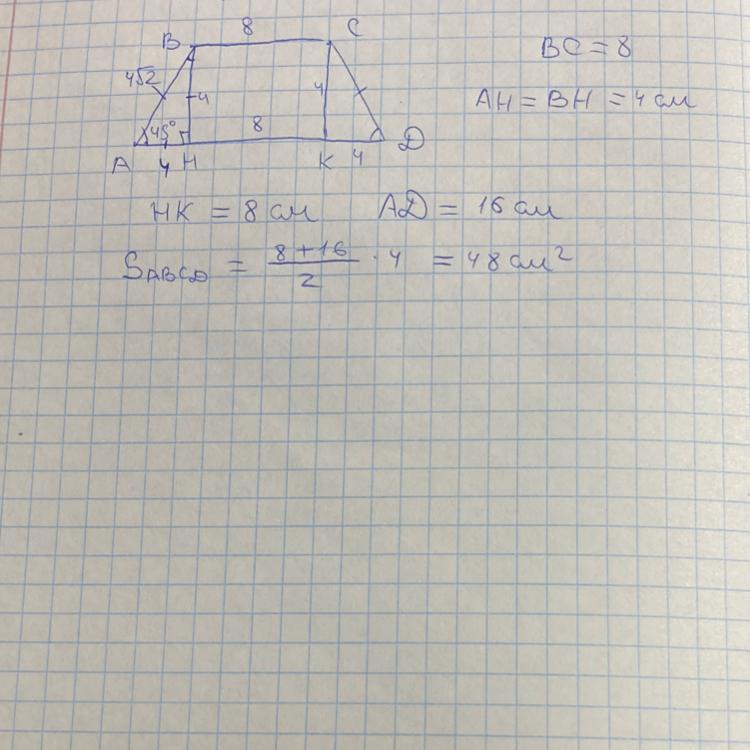
Менша основа рівнобічноï трапеції дорівнює 8 см, а її висота-4 см, гострий кут дорівнює 45°. Знайдіть площу трапеції. ​

Answer 1

Для знаходження площі трапеції потрібно спочатку знайти довжини бічних сторін трапеції за заданими даними.

Оскільки кут між основою та бічною стороною трапеції дорівнює 45°, то можна скористатися властивостями рівнобедреної трапеції та побудувати прямокутний трикутник, який має бічну сторону трапеції як гіпотенузу та кут 45° між гіпотенузою та меншою основою трапеції.

За теоремою Піфагора, довжина бічної сторони трапеції дорівнює:
$$
\sqrt{8^2 + 4^2} = \sqrt{80} = 4\sqrt{5}.
$$

Далі, за формулою для площі трапеції:
$$
S = \frac{(a + b)h}{2},
$$
де $a$ та $b$ - довжини основ трапеції, а $h$ - її висота, маємо:
$$
S = \frac{(8 + 4\sqrt{5}) \cdot 4}{2} = 16 + 8\sqrt{5} \approx 34.31 \text{ см}^2.
$$

Отже, площа рівнобічної трапеції дорівнює близько 34.31 квадратних сантиметрів.

Answer 2

вдвдіжвжвжвжввжжвжвжвжвдввддвх