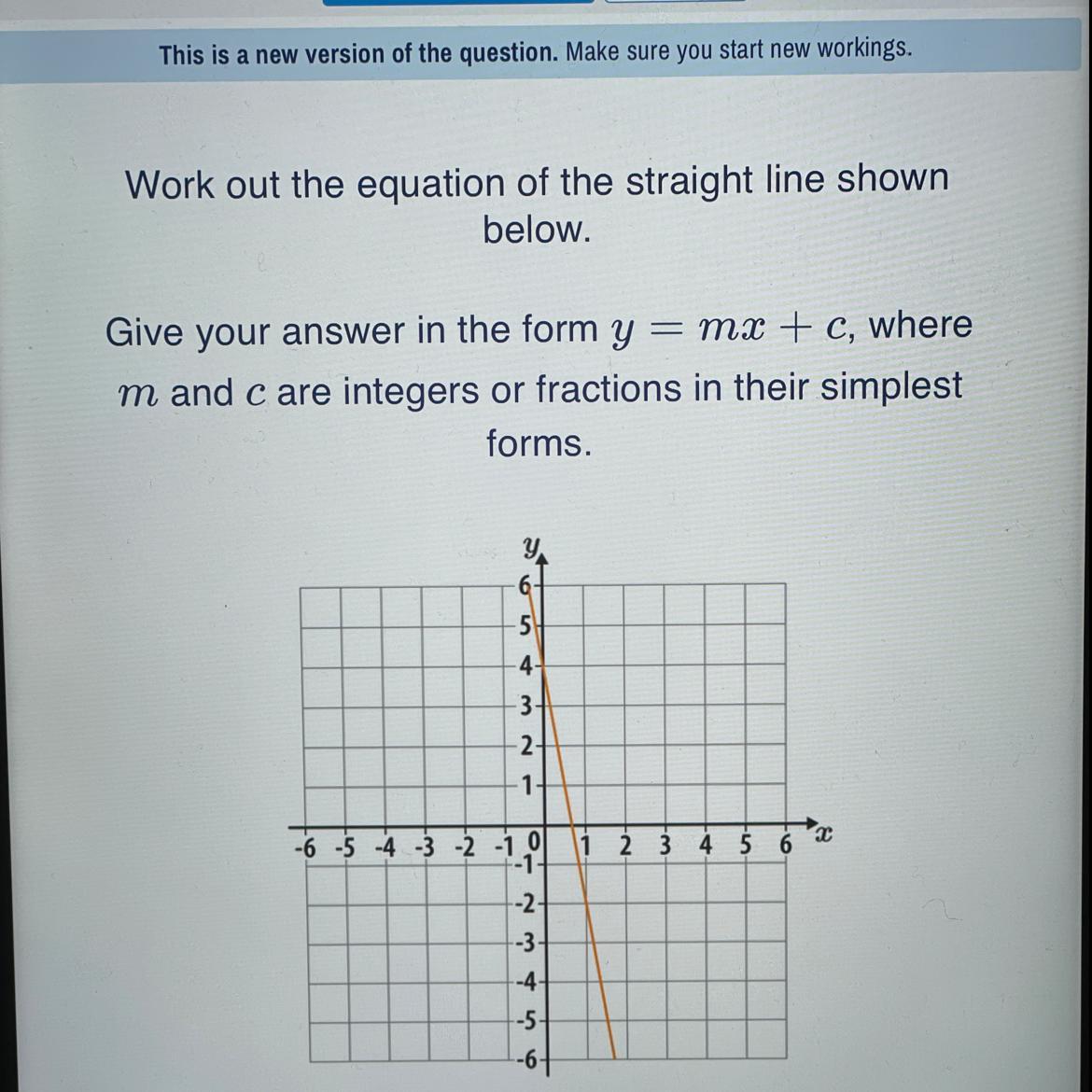
Work out the equation of the straight line shown
below.
Give your answer in the form y = mx + c, where
m and c are integers or fractions in their simplest
forms.
Ответы
Відповідь:
To work out the equation of a straight line, we need to know the slope (m) and the y-intercept (c).
If we have the coordinates of two points on the line, we can use the formula:
m = (y2 - y1) / (x2 - x1)
Once we have the slope (m), we can substitute one of the points and the slope into the equation:
y = mx + c
Let's say we have the points (x1, y1) and (x2, y2) on the line. We can calculate the slope using the formula:
m = (y2 - y1) / (x2 - x1)
Then, we can substitute one of the points and the slope into the equation:
y = mx + c
For example, let's say we have the points (2, 5) and (4, 9) on the line.
First, we calculate the slope (m):
m = (9 - 5) / (4 - 2)
m = 4 / 2
m = 2
Now, we substitute one of the points (let's use (2, 5)) and the slope (m) into the equation:
5 = 2(2) + c
Simplifying:
5 = 4 + c
Now, we solve for c:
c = 5 - 4
c = 1
Therefore, the equation of the straight line is:
y = 2x + 1