Question

даю 50 баллов за хорошее и понятное объяснение

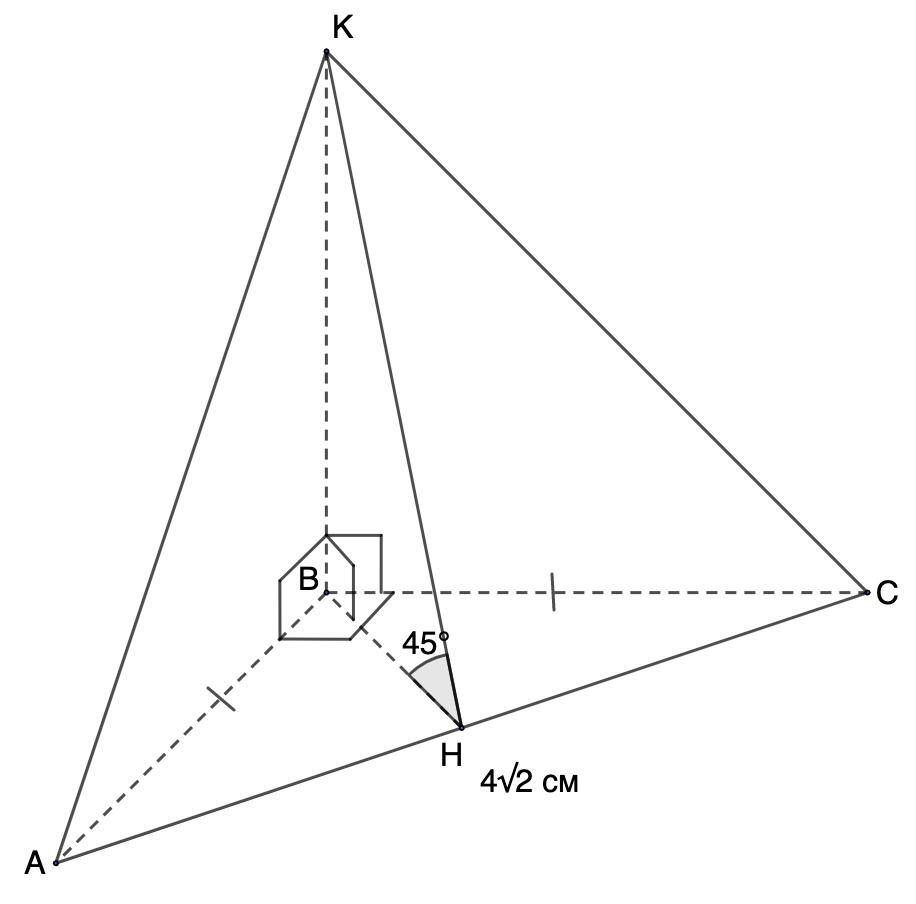
Основание пирамиды - равнобедренный прямоугольный треугольник с гипотенузой 4√2см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания,

а третья грань наклонена к ней под углом 45°.

А) Найдите длины боковых ребер пирамиды.

Б) Найдите площадь боковой поверхности пирамиды.

Answer 1

Ответ:

А) Длины боковых ребер пирамиды равны: КВ = 2√2 см, АК = КС = 2√6 см.

Б) Площадь боковой поверхности пирамиды равна 16√2 см²

Пошаговое объяснение:

Основание пирамиды - равнобедренный прямоугольный треугольник с гипотенузой 4√2 см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45°.

А) Найдите длины боковых ребер пирамиды.

Б) Найдите площадь боковой поверхности пирамиды.

Дано: КАВС - пирамида;

ΔАВС - прямоугольный, равнобедренный;

АС = 4√2 см - гипотенуза;

АКВ ⊥ АВС; ВКС ⊥ АВС.

АКС наклонена к АВС под углом 45°.

Найти: А) КА, КВ, КС.

Б) Sбок.

Решение:

Определимся с углом наклона АКС к АВС.

• Угол между плоскостями - угол между перпендикулярами, проведенными в данных плоскостях к линии пересечения плоскостей.

Проведем высоту ВН и соединим Н и К.

• Если каждая из двух пересекающихся плоскостей перпендикулярна третьей плоскости, то линия пересечения данных плоскостей перпендикулярна третьей плоскости.

КВ ⊥ АВС   ⇒   ВН - прекция НК на (АВС)

• Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.

⇒ КН ⊥ АС

⇒ ∠КНВ = 45° - искомый угол.

А) Найдем боковые ребра.

Рассмотрим ΔАВС - прямоугольный, равнобедренный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ВАС + ∠ВСА = 90°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ВАС = ∠ВСА = 90° : 2 = 45°

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin \;45^0 =\frac{BC}{AC};\;\;\;\frac{\sqrt{2} }{2} =\frac{BC}{4\sqrt{2} } ;\;\;\;BC=\frac{\sqrt{2}\cdot4\sqrt{2} }{2}=4\;_{(CM)}$

⇒ AB = BC = 4 см.

Рассмотрим ΔАВН - прямоугольный.

$\displaystyle sin \;45^0 =\frac{BH}{AB};\;\;\;\frac{\sqrt{2} }{2} =\frac{BH}{4 } ;\;\;\;BH=\frac{\sqrt{2}\cdot4 }{2}=2\sqrt{2} \;_{(CM)}$

Рассмотрим ΔВКС - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\;45^0=\frac{KB}{BH};\;\;\;1=\frac{KB}{2\sqrt{2} } ;\;\;\;KB=2\sqrt{2}\;_{(CM)}$

По теореме Пифагора найдем НК:

HK² = BK² + HB² = 8 + 8 = 16   ⇒   HK = 4 (см)

Рассмотрим ΔАКВ и ΔВКС - прямоугольные.

КВ - общая; АВ = ВС (условие)   ⇒   ΔАКВ = ΔВКС (по двум катетам)

По теореме Пифагора из ΔАКВ найдем АК:

АК² = КВ² + АВ² = 8 + 16 = 24   ⇒   АК = √24 = 2√6 (см)

Длины боковых ребер пирамиды равны: КВ = 2√2 см, АК = КС = 2√6 см.

Б) Найдем площадь боковой поверхности.

Sбок. = S(AKB) + S(BKC) = S(AKC)

• Площадь прямоугольного треугольника равна половине произведения катетов.

$\displaystyle S(AKB)=\frac{1}{2}AB\cdot BK = \frac{1}{2}\cdot 4\cdot 2\sqrt{2}=4\sqrt{2} \;_{(CM^2)}$

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(AKC)=\frac{1}{2}AC\cdot KH=\frac{1}{2}\cdot 4\sqrt{2}\cdot 4 = 8\sqrt{2} \;_{(CM^2)}$

S(AKB) = S(BKC) = 4√2 см²

⇒ Sбок. = 4√2 + 4√2 + 8√2 = 16√2 см²

Площадь боковой поверхности пирамиды равна 16√2 см²