В трапеции ABCD, ∠BAD=90°, ∠АВС=arctg2; AB=BC. Квадрат KLMN расположен в пространстве так, что его центр совпадает с серединой отрезка АВ. т.А є LK, AL>AK, т.М равноудалена от точек A и D. Расстояние от точки L до ближайшей к ней точки трапеции ABCD равно 3/2,а расстояние от точки N до ближайшей к ней точки трапеции равно √6. Найдите площадь трапеции и расстояние от точки М до плоскости ABCD.

Ответы
Ответ:
S(ABCD)=45
MM1 =√(33/5)
Объяснение:
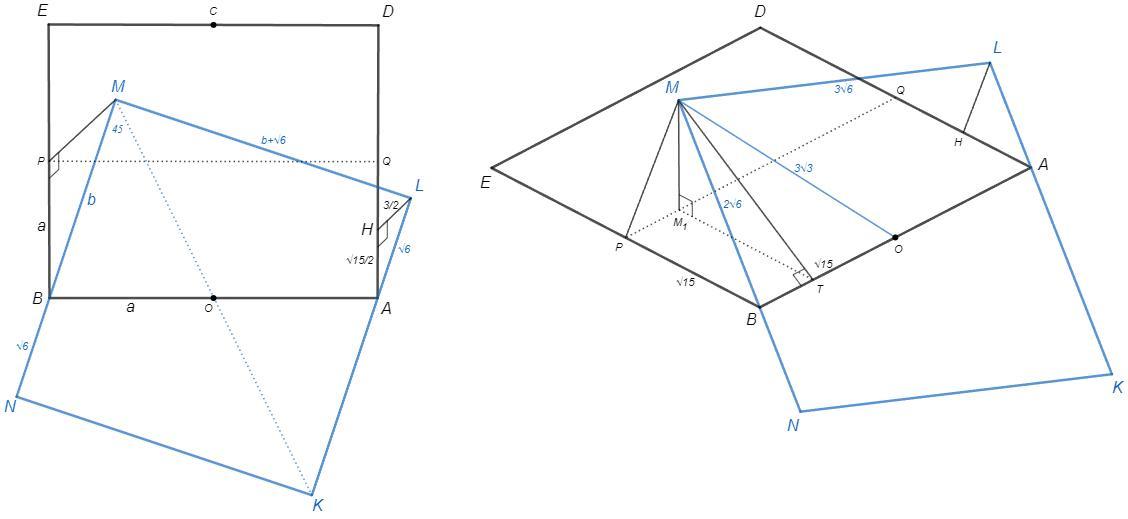
CO⊥AB , CO=AD=AB
CO/BO=tgABC=2 => AB/BO=2 => O - середина AB
Будем рассматривать квадрат ABED, трапеция равна 3/4 его площади.
Пусть P и Q - середины сторон BE и AD
Точка M лежит в серединно-перпендикулярной плоскости отрезков BE и AD.
(PMQ)⊥(ABD) , MP⊥BE
Точка B симметрична точке A относительно центра O, следовательно лежит на стороне MN.
BN - кратчайшее расстояние от N до отрезка AB (без доказательства)
BN=AL (симметрия) =√6
LH⊥AD , LH=3/2
AH =√(AL^2 -LH^2) =√15/2
BP=BO=a , BM=b
ML=b+√6 , MO=ML/√2 =(b+√6)/√2
△ALH~△BMP (стороны параллельны)
a/b =√15/2 : √6 =√(5/8)
△BMO, т косинусов:
BO^2 =BM^2 +MO^2 -2BM*MO cos45 => a^2 =b^2/2 +3
разделим на b^2
(a/b)^2 =1/2 +3/b^2 => 5/8 =1/2 +3/b^2 => b^2=24
=> b=2√6 ; a=√15
AB=2√15 ; S(ABED)=AB^2=60
S(ABCD)=3/4 S(ABED)=45
MT⊥AB , MM₁⊥(ABD)
MO=3√3 ; BO=BP=M₁T=√15 ; MB=2√6
△BMO, т синусов
MO/sinMBO =BO/sin45 => sinMBO=3/√10
MT=MB sinMBO =6√3/√5
MM₁ =√(MT^2 -M₁T^2) =√(36*3/5 -15) =√(33/5)